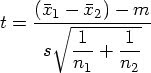SAS SGPLOT for creating statistical graphs

For a long time, we have been using SAS GPLOT for creating graphs. Beginning from SAS version 9.2, there is a new procedure called SAS SGLPOT, which could be a good tool for statisticians.

The detail about this procedure is described in SAS onlind document. There are several white papers about using this procedure.

• SAS/GRAPH® Procedures for Creating Statistical Graphics
  in Data Analysis
• SAS blog talking about SGPLOT procedure
• Using PROC SGPLOT for Quick High Quality Graphs

Subject Diaries in Clinical Trials

Subject Diary, often called Patient Diary, is a tool used in the clinical trials. There could be three types of diary technologies. The traditional approach has been to use paper cards or booklets configured to help the subject follow directions from the clinical protocol. More recently, electronic means have been used, such as dial-in phone numbers with computer-driven questions to answer (interactive voice response systems, IVRS) and handheld devices with alarms and menu-driven prompts to guide the subject through the protocol requirements - e-diaries.

In 2006, FDA issued a draft Guidance for Industry "Patient-Reported Outcome Measures: Use in Medical Product Development to Support Labeling Claims" This guidance describes how the FDA evaluates patient-reported outcome (PRO) instruments used as effectiveness endpoints in clinical trials. Here the patient-reported outcome is typically collected through subject diary. However, the use of subject diary to collect the information on efficacy is just one of many usages. Subject diary can also be used to collect the information about:

• Daily symptoms, dialy activities
• Safety assessment (such as adverse events, exacerbations)
• Usage of the study medication to measure the compliance
• Usage of the concomitant medication
• Disease episodes on daily basis

Diary does not have to be filled out on daily basis. There are studies using diary and the subjects write down in a diary each time they take the medication,

FDA guidance listed three reasons to collect the data reported by the subject:

• Some treatment effects are known only to the patient;
• There is a desire to know the patient perspective about the effectiveness of a treatment;
• Systematic assessment of the patient’s perspective may provide valuable information that can be lost when that perspective is filtered through a clinician’s evaluation of the patient’s response to clinical interview questions.

The drawback of the diary data is the reliability of the data or the quality of the data. Subject could lose the diaries, forget to complete them or forget to complete the diaries in real time, and in worse situation, falsify information. To ensure that subject diaries comply with GCP standards, the followings are critical (adapted from Good Clinical Practice: A Question & Anwer reference)

"At the beginning of a study, site staff should explain to each subject (or parent) the importance of the diary and how the subject should record data within it. Site staff should review the diary at each visit; deficiencies and attempts to correct these deficiencies should be noted in source records. Site staff must ensure that the diaries are returned at the time designated in the trial protocol. If a patient diary is not returned, the site should make several attempts to retrieve it. These attempts should be documented in the subject’s medical record.

Although clinical auditors and FDA inspectors recognize that diaries often pose a source documentation problem, they expect to see documented efforts to minimize these problems. Diaries that are too neat, all look the same, or have been rewritten by the study coordinator are sure to raise suspicious. "

Subject diary data is often subjected to the audit findings. For example, in one of FDA's warning letters, it cited the violation about subject diary data.

"Protocol (b)(4) specified that subjects were to be distributed patient daily diary cards every 4 weeks, beginning with Week 0, and ending on Week 53. Per the protocol, patients should only have received one set of diary cards for each four-week period. However, during its inspection, FDA discovered that your records contained multiple diary entries for the same subjects on the same dates. Furthermore, the information you reported to the CRF excluded some of the data from one or more sets of patient diaries. This is a violation of 21 CFR 312 .70.
Protocol (b)(4) specified that the study coordinator was to review the patient diary cards with the patient during each scheduled visit and, if possible, query the patient to obtain any missing information at the scheduled visit. Thus, patient diaries should have only contained dated entries for dates that occurred between two scheduled visits.
The daily diary cards included information concerning whether the subject took the doses of medication in the morning and the evening (diary question #1), whether any concomitant medications were taken (diary question #2), the name of the concomitant medication taken (diary question #3), usual daily activity interruptions due to (b)(4 ) pain (diary question #4), whether any medical facility was visited due to ( b) (4) pain (diary question #5), the name of the medical facility visited (diary question 7T6), and the daily pain level experienced on a scale of 0 to 10 (diary question #7). Per the protocol, information in patient diary cards was to be recorded onto the appropriate case report form (CRF).
FDA's audit identified that 2 of 12 subjects enrolled in the study, Subjects #003 and #0 10, had two sets of patient diaries which contained different information for the same dates . From our review of the two sets of patient diaries, we were unable to determine which diary provided the correct information. In addition, we note that the information reported to the CRF was either (1) obtained from one diary but not the other, or (2) could not be verified in our review of either version of the duplicate diaries' entries for specified dates. The discrepancies we observed included, but were not limited to, the following: ...."

In terms of the handling of the subject or patient diary data, there are many different ways depending on the diary technology and the purpose of the diary. Subject diary data could be directly transmitted to the data management group without review by the site investigator or study coordinator. The data clarification (query) process is omitted. For example, in a study with Irritable Bowel Symdrome, diary data collected through IVRS was directly transferred to teh data management group and biostatistics group for analysis. Subject diary data could also be collected by the site and reviewed by the site staff (investigator or study coordinator). In this situation, the subject diary is a tool to assist the site staff in evaluating the subject about the disease status, any significant event, drug compliance,... For example, the subject diary could used to collect the COPD exacerbation (subjects record the dialy symptoms, antibiotic use, steroid use,...). in this case, the subject diary should be periodically reviewed by the site staff.

Box-Cox Transformaton

In statistical / biostatistical analysis, it is pretty common to apply the data transformation technique. The reason is to achieve the normality assumption. data transformation refers to the application of a deterministic mathematical function to each point in a data set — that is, each data point zi is replaced with the transformed value yi = f(zi), where f is a function.

The typical data transformations include logarithm, square root, Arcsine transformation. Log transformation is suitable for variables with log-normal distributions. The square-root transformation is commonly used when the variable is a count of something. For arcsin transformation, the numbers to be transformed must be in the range −1 to 1. This is commonly used for proportions, which range from 0 to 1.

Another popular data transformation technique Box-Cox transformation, which we may not use frequently in clinical trials. Box-Cox transformation belongs to the so-called 'power transform'. The Box-Cox family of transformations has two useful features: first, it includes linear and logarithmic transformations as special cases; and, second, it possesses strong scale equivariance properties, including the property that the transformation parameter is unaffected by the rescaling. Application of the Box-Cox transformation algorithm reduced the heterogeneity of error and permitted the assumption of equal variance to be met. Its main disadvantage is that both the domain and the range of the transformation are, in general, bounded.

Box-Cox transformation can be easily implemented with SAS Proc Transreg.

Further readings:

• Box-Cox Transformation: an Overview by Pengfei Li

• Basic Box-Cox Transformations using SAS Proc Transreg
• A Box-Cox Transformation using SAS Stat Studio
• What to do when data are non-normal?

Dealing with the paired data

Paired data contains values which fall normally into pairs and can therefore be expected to vary more between pairs than within pairs. The pairing is to reduce the variability. After the pairing, The between-subject variability will be eliminated. If pairing is effective it will reduce variability enough to justify the effort involved to obtain paired data.

There are many practical examples of paring. In clinical trial, crossover design is a special case of the pairing where the same subject receive more than one treatment. If all subjects receive treatment A, then treatment B, it can still be called crossover design (single sequence cross over design). In Epidemiology field, the case-control study is typically paring. There are terms 1:1 matched case-control, and 1:m matched case-control. In education, we can do the paring to compare the scores before and after the training;......

When outcome measures are continuous variable (such as drug concentration), without considering the covariates, analysis of paired data can be implemented by using paired t-test which can be easily performed using SAS PROC UNIVARIATE (calculate the difference for each pair, then run PROC UNIVARIATE) or SAS PROC TTEST (without calculating the difference first). Suppose x1 and x2 are paired variables,

proc ttest;
 paired x1*x2;
run;

If the normality assumption is questionable, the non-parametric tests (sign test and Wilcoxon signed rank sum test) can be used. UCLA's Statistical Consulting Services web site provided examples for these tests.

In more complicated situation (such as crossover design) or if we have to do the modeling to include the covariates, mixed model needs to be used. SAS PROC MIXED can implement the mixed model easily. See SAS/Stat User's Manual for PROC MIXED. In a research paper titled "Detection of emphysema progression in alpha 1-antitrypsin deficiency using CT densitometry; Methodological advances", I actually dealt with the paired data using so called 'random coefficient model'.


When outcome variable is discrete data, the easiest example is McNemar test. McNemar's test is performed if we are interested in the marginal frequencies of two binary outcomes. These binary outcomes may be the same outcome variable on matched pairs (like a case-control study) or two outcome variables from a single group.

In more complicated situation or if the covarites need to be included in the model, 'conditional logistic regression' needs to be employed. 'Conditional logistical regression' can be implemented using SAS Proc Logistic or SAS Proc PHREG. See following links for detail descriptions.

• A Tutorial on Logistic Regression by Ying So in SAS

• Condition Logistic Regression using SAS Proc PHREG procedure by David Brown

Pediatric use and geriatric use of drug and biological products

In the United States, every marketed drug or biological product needs to have its product label or package insert. The product label contains the use in special populations including pediatric and geriatric population. Here is a paragraph from FDA guidance on "Labeling for Human Prescription Drug and Biological Products — Implementing the New Content and Format Requirements"

Use in Specific Populations (§ 201.57(a)(13))
Information under the Use in Specific Populations heading includes a concise summary
of any clinically important differences in response or recommendations for use of the
drug in specific populations (e.g., differences between adult and pediatric responses, need
for specific monitoring in patients with hepatic impairment, need for dosing adjustments
in patients with renal impairment). Typically, information under this heading includes
limitations or precautions for specific populations or established differences in response.

Absence of the clinical study data in pediatric and geriatric population could sometimes cause problems in product label or in the drug approval process. During the drug development process, it is prudent to consider the inclusion/exclusion of patient population in terms of the age limit. In the study protocol, the inclusion criteria pertinent to the age limits (upper and lower limits) should be carefully considered. In the statistical analysis, when data for pediatric and/or geriatric population is available, subgroup analysis should always be performed.

In regulatory environment, the classification of the pediatric and geriatric population are defined as:

Pediatric population: according to ICH guidance E11 "Clinical Investigation of Medicinal Products in the Pediatric Population", the pediatric population contains several sub-categories:

• preterm newborn infants
• term newborn infants (0 to 27 days)
• infants and toddlers (28 days to 23 months)
• children (2 to 11 years)
• adolescents (12 to 16-18 years (dependent on region))

Notice that in FDA's guidance "General Considerations for Pediatric Pharmacokinetic Studies
for Drugs and Biological Products", the age classification is a little bit different. I am assuming that the ICH guidance E11 should be the correct reference.
Geriatric population:
Geriatric population is defined as persons 65 years of age and older. There is no upper limit of age defined. The Food and Drug Administration has regulations governing the content and format of labelling for human prescription drug products, including biological products, to include information pertinent to the appropriate use of drugs in the elderly and to facilitate access to this information by establishing a “Geriatric use” subsection in the labelling.

Further readings:

• Regulatory requirements for the development of medicinal products for pediatric use by Dr. Tom Sam
• FDA good review process "Labeling for Human Prescription Drug and Biological Products — Determining Established Pharmacologic Class for Use in the Highlights of Prescribing Information"
• FDA's Pediatric Drug Development
• Pediatric Trials: a Worldview

GxP: a collection of quality guidelines in clinical trial

GxP is now used to represent a collection of quality guidelines in clinical trial. The titles of these good practice guidelines usually begin with "Good" and end in "Practice", with the specific practice descriptor in between. A "c" or "C" (stands for 'current') is sometimes added to the front of the acroynm to form cGxP. For example, cGMP is an acronym for "current Good Manufacturing Practices."

Professionals who are working in the pharmaceutical or biotechnology industry should be very familiar with three common GxPs: GCP, GMP, and GLP.

GCP: Good Clinical Practices is an international ethical and scientific quality standard for designing, conducting, recording and reporting trials that involve the participation of human subjects. The GCP is governed by ICG guideline E6. To learn more about GCP, watch the GCP 101: An introduction at FDA website.

http://www.fda.gov/Training/CDRHLearn/ucm176411.htm

GLP: Good Laboratory Practice. Refer to Wikipedia for detail. GLP is the guidance for laboratory tests, pre-clinical tests, bioanalytical assays/measures, toxicology tests,...

cGMP: current Good Manufacturing Practice regulations for drugs contain minimum requirements for the methods, facilities, and controls used in manufacturing, processing, and packing of a drug product. FDA has many guidance on cGMP.

Recently, many other GxP terms have surfaced. It looks like that each functional area in clinical trial will have its own GxP. Below are some examples: GRP, GPP, GSP, and GCDMP.

GRP: Good Reprint Practices. In January 2009, FDA issued its final version of the guidance "Good Reprint Practices for the Distribution of Medical Journal Articles and Medical or Scientific Reference Publications on Unapproved New Uses of Approved Drugs and Approved or Cleared Medical Devices"

GPP: Good Pharmacovigilance Practices. In 2005, FDA issued its guidance on "Good Pharmacovigilance
Practices and Pharmacoepidemiologic Assessment" to provide guidance on (1) safety signal identification, (2) pharmacoepidemiologic assessment and safety signal interpretation, and (3) pharmacovigilance plan development.

While GRP and GPP are proposed by the regulatory agencies, there is no officially issued guidance on GSP (Good Statistical Practices) and GCDMP (Good Clinical Data Management Practices). However, the principles of these two good practices have been largely covered in ICH guidances, specifically, E9 (Statistical Principles for Clinical Trials) and E6 (Good Clinical Practice).

PSI Professional Standards Working Party developed a GUIDELINES FOR STANDARD OPERATING PROCEDURES for Good Statistical Practice in Clinical Research.

In several DIA presentations, Good Statistical Practices were said to include the following components:

Science:

• Protocol – Minimize bias – Maximize precision
• Analysis plan
• Presentation of results
• Leadership

Operational Processes

• Controlled statistical environment
  
• SOPs • Productivity tools
  
• Data standards
  
• Training
  

Credibility Results

• Reproducible research
  
• Transparent and efficient processes
  
• Validated analysis
  
• Data integrity assurance
  

The Good Clinical Data Management Practices (GCDMP) is developed by the SCDM (Society of Clinical Data Management). It provides assistance to clinical data managers in their implementation of high quality clincal data management processes and is used as a reference tool for clinical data managers when preparing for CDM training and education.

Biostatistics conferences/workshops

When I started my career in biostatistics, I joined the American Statistical Association (ASA) and attended its annual meeting (Joint Statistical Meeting) rotated in different large cities in North America (US and Canada). I have enjoyed the atmoshpere of the conference and networked with friends and professors in the statistical field.

For two consective years, I have skipped the meeting. Instead, I attended the FDA/Industry Statistical Workshop. JSM may be good to the students, but may not be good for professions (especially for statisticians who are working in drug development area). JSM has a lot of sessions/presentions that are unfiltered and too theoretic. A lot of stuff may never have the value in application. Even though it may be applicable one day, it may not be acceptable to the regulatory agencies.

The statistical conferences, symposiums, workshops with focus on clinical trial and drug development have thrived in recent years. Twice a year, FDA holds its workshops: one with Drug InformationAssociation "FDA/industry statistical forum" and one with ASA "FDA/industry statistical workhop". These conferences are more specific to the biopharmaceutical field and the topics are more relevant to the daily work of biostatisticians.

There are also several societies with focus on biostatics, for example, the International Society for Biopharmaceutical Statistics (ISBS) and the International Society for Clinical Statistics (ISCS). The International Chinese Statistical Association (ICSA) is also adjusting its focus to the biopharmaceutical field. Within ASA, biopharmaceutical network has been formed.

To get a flavor of the topics in these meetings, see the following links:

• 2009 FDA/Industry Statistical Workshop online program and presentations (The password to view presentations is Capitol
• Biopharmaceutical network's webinar topics and handouts

Positive Psychology - science to find happiness

When I see a news headline about "what is the most popular course in the Harvard University?", my curiosity drives me to find out what the course is. This leads me to the concept of "Positive Psychology". The most popular class is the Psychology 1504 (ie, positive psychology) taught by Dr. Ben-Shahar.

As mentioned in NPR news, "almost every semester for the past ten years, the most popular class at Harvard has been Intro to Economics, or as Tal Ben-Shahar likes to call it, how to get rich, but today there's an even bigger class on campus. It's Ben-Shahar's course on what he calls, how to get happy."

According to Wikipedia, Positive psychology is a recent branch of psychology that "studies the strengths and virtues that enable individuals and communities to thrive". Positive psychologists seek "to find and nurture genius and talent", and "to make normal life more fulfilling", not simply to treat mental illness. In other words, the positive psychology deals with love, happiness, job satisfaction, ...

In contrary to the Positive psychology, there should be a concept of negative psychology. However, even though the current psychology is so focused on the negative side (depression, fear, anxiety, mental illness,...), there is no formal definition of negative psychology.

Further readings about the negative psychology:

• The website of Tal Ben-Shahar
• Tal Ben-Shahar's video on Youtube
• Dr Seligman's vedio on Youtube
  
• NPR report on finding happiness
• Harvard psychology course information (including course slides)
• UPenn's Positive Psychology Center
• Good Life: Happiness on Youtube
  

Unlike the negative psychology which belongs to the medical science, the positive psychology has its applications in corporate business. It could be used to promote the positive culture, attitudes, employee's job satisfaction,...

However, there is also negative side about the positive psychology. See Dr. BARBARA S.HELD's argument.

In practice, Positive psychology encompass a variety of techniques that encourage people to identify and further develop their own positive emotions, experiences, and character traits. In many ways, positive psychology builds on key tenets of humanistic psychology. Whether or not the positive psychology techniques work will eventually rely on the evidence from the clinical trials. Since the psychology measures are typically intangible, how to design a trial or intervention, what to measure, how long to measure, what instrument to use,... could be challenging even more than the typically psychology measures (with the focus on disease or negative psychology). The following paper discussed this issue.

Overtreated, excess care

"Overtreated", "Overdiagnosed", and "Overdosed",... these are the terms I have used in one of seminars several years ago. By comparing the health care system between the United States and the China, you could easily think of these terms, especially when I heard the new medical conditions "ADHD - Attention-Deficit Hyperactivity Disorder", "M-IBS - Mixed Irritable Bowel Syndrome", "Chronic Fatigure Syndrome (CFS)", "fibromyhalia"; when I saw the images how many pills a patient took regularly.

Driven by the NPR interview with Shannon Brownlee (Are Today's Hospital Patients "Overtreated"?), I went to the local library to borrow her book "Overtreated: why to much medicine is making us sicker and poorer". I enjoyed very much in reading this book.

I intended to write a blog about this book, then found that many people had already expressed their opinion about this book. See Book Reviewer's comments from Amazon

Even though this book was written two years ago (in 2007), the arguments, the facts, the reasoning described in this book is very much relevant to the situation today (when the debate on the health care reform heats up). Below is a list of chapters:

• One: Too Much Medicine
• Two: The Most Dangerous Place
• Three: Your Local Hospital
• Four: Broken Hearts
• Five: The Desperate Cure
• Six: The Limits of Seeing
• Seven: The Persuaders
• Eight: Money, Drugs, and Lies (my favorite chapter)
  
• Nine: The Doctor Isn't In
• Ten: Less is More

Instead of going to detail, I would just cite some sentences from the book:

• "Doctors have a saying: Never get admitted to a teaching hospital in July, because that's when all the new interns arrive fresh from medical schools."
• "As research would show over the coming decades, stunningly little of what physicians do has ever been examined scientifically, and when many treatments and procedures have been put to the test, they have turned out to cause more harm than good."
• "Every patient admitted to a hospital risks being hurt or even killed by the very people who wish to help her."
• "Even as the number of [medical] imaging tests [X-ray, CT, MRI] is going up, numerous studies suggest that all those pictures are not nearly as effective at improving diagnosis as many doctors--and patients--tend to think."
• "The drug company representative, or drug rep, usually [is] a handsome young man or shapely young woman who has been recruited more for his or her good looks and outgoing personality than for his or her aptitude for science or medicine."
• "Among drug reps the unofficial name for thought leaders who work for multiple companies is 'drug whores'"
• "The more specialists involved in your health, the more likely it is that you will suffer from a medical error, that you will be given care you don't need and be harmed by it."
• "The Institute of Medicine estimates that only 4 percent of treatments and tests are backed up by strong scientific evidence; more than half have very weak evidence or none."
• "In the view of Richard Horton, a British physician and editor of the prestigious medical journal the Lancet, 'Journals have devolved into information-laundering operations for the pharmaceutical industry'"
• Says John abramson "The primary mission of medical research has been transformed. It used to be all about gathering information to improve health. Now clinical research is aimed at gathering information that will maximize return on investment"
  

Further readings:

• Are Americans Seeing Their Doctors Too Often? by Shannon Brownlee
• Overtreated blog by Shannon Brownlee
• Getting Well: It's About Time by Melinda Beck "Americans spend billions of dollars a year to treat things that would go away on their own."
• HARLOT plc: an amalgamation of the World's Two Oldest Professions by David Sackett and Andrew Oxman. BMJ
• Overdosed America: The Broken Promise of American Medicine by John Abramson

Reporting pregnancies during clinical trials

Unless a clinical trial is designed for the pregnancy women, the typical clinical trial will exclude the females with pregnancy and lactating. In either the inclusion or exclusion criteria, there will be one criterion related to the exclusion of female subjects with pregnancy. The wording for inclusion or exclusion criteria varies. Here are some examples:

Inclusion criteria:

"Women of childbearing age must have a negative pregnancy test and must useadequate contraception during the treatment phase of the study and for 9months afterwards. Women who wish to breast feed are not eligible for thestudy"

"Females must be of non-childbearing potential. Women of non-childbearing potential are defined as those who have no uterus, ligation of the fallopian tubes, or permanent cessation of ovarian function due to ovarian failure or surgical removal of the ovaries. Documentation of surgical procedure or physical examination is required for subjects who have had a hysterectomy or tubal ligation. In the absence of such documentation, a urine pregnancy test is required for inclusion into the study. A woman is also presumed to be infertile due to natural causes if she has been amenorrheic for greater than 12 months and has an FSH greater than 40 IU/L"

Exclusion criteria:
"Pregnant or nursing (lactating) women, where pregnancy is defined as the state of a female after conception and until the termination of gestation, confirmed by a positive hCG laboratory test (>= 5 mIU/mL) "

"Pregnant or breast-feeding patients. Women of childbearing potential must have
a negative pregnancy test performed within seven days prior to the start of study
drug. Both men and women enrolled in this trial must use adequate birth control"

The females that are childbearing potential are typically allowed to be enrolled in the clinical trials as long as they are willing to practice a highly effective method of contraception (oral, injectable or implanted hormonal methods of contraception, placement of an intrauterine device [IUD] or intrauterine system [IUS] condom or occlusive cap with spermicidal foam/gel/film/cream/suppository, male sterilization, or true abstinence) throughout the study.

However, it is not uncommon to have female subjects who become pregnant during a clinical investigation. In such instances, should the pregnancy be reported as AE or SAE?

The answer depends on the outcome of the pregnancy (either on mother side or on fetus side).

Pregnancy occurring during a patient’s participation in a clinical trial, although not
typically considered an SAE, must be notified to the sponsor within the same timelines as an
SAE (within one working day) on a Pregnancy Monitoring Form. The
outcome of a pregnancy should be followed up carefully and any abnormal outcome
of the mother or the child should be reported. This also applies to pregnancies
following the administration of the investigational product to the father prior to
sexual intercourse.

Based on the outcome and the timing of the delivery, the pregnancies during the clinical trial can be categoried into the followings:
Female is study participant and becomes pregnant during study participation:

1. Normal outcome before end of study
2. Abnormal outcome before end of study
3. Normal outcome after end of study
4. Abnormal outcome after end of study

Female is partner of study participation and becomes pregnant during study:

5. Normal outcome before or after end of study

6. Abnormal outcome before or after end of study

In all of these situations, the Pregnancy Monitoring Form should always be filled out. However, only for situation #2, a SAE needs to be reported.

Since the typical clinical trials do not include the pregnancy women, the potential impact of the drug on pregnancy women is not obtained during the pre-market studies. A lot of drug labels contain a statement in the contradiction section about the pregancy women. Drug exposure could also have impact on fetus - a term called 'Teratogenicity'. Teratogenicity refers to the capability of a drug to cause fetal abnormalities when administered to the pregnant mother. One of the best-known examples of such a drug- induced birth defect is the Thalidomide disaster. The drug was prescribed on a wide scale to pregnant mothers to ease the anxiety associated with it. The large-scale consumption of the drug resulted in children born with seal like limbs, often referred to as phocomelia. The drug was banned for prescription in 1961.

The potential impact of the drug on pregnancy could be obtained from observational studies - pregnancy registries. Refer to FDA's website about "General Information about Pregnancy Exposure Registries".

In ICH E2D "Post-Approval Safety Data Management: Definitions and Standards for Expedited Reporting", the following paragraph is stated:

"5.4.1 Pregnancy Exposure
MAHs (market authorization holders) are expected to follow up all pregnancy reports from healthcare professionals or consumers where the embryo/foetus could have been exposed to one of its medicinal products. When an active substance, or one of its metabolites, has a long half-life, this should be taken into account when considering whether a foetus could have been exposed (e.g., if medicinal products taken before the gestational period should be considered). "

A sample pregnancy registry form can be found from GSK website.

Conficence Interval vs. Credible Interval

I recently participated in a project to compare two different ways to do the meta analysis: the traditional way to pool the database directly (sort of the integrated analysis) and the Bayesian approach (prior distribution + likelihood function -> posterior distribution). When we try to compare the results from two different approaches, we run into the issue of comparing 'confidence interval' and 'credible interval'. While these two terms have some similarities, the interpretations are quite different.

The "confidence interval" is a term used by frequentist - I am a frequentist. If we say an estimate has its 90% confidence interval of 35-45, it means that with a large number of repeated samples, 90% of times, the true value of the parameter will fall within the range of 35-45.

The term 'credible interval' is used by Bayesian statisticians and it may also be called 'Bayesian Posterior Interval'. In Bayesian statistics, a credible interval is a posterior probability interval, used for purposes similar to those of confidence intervals in frequentist statistics. Bayesian inference is statistical inference in which probabilities are interpreted not as frequencies or proportions or the like, but rather as degrees of belief. ...

The posterior probability can be calculated by Bayes theorem from the prior probability and the likelihood function. ... In statistics, a confidence interval (CI) is an interval between two numbers, where there is a certain specified level of confidence that a population parameter lies. ... Statistical regularity has motivated the development of the relative frequency concept of probability. ...

For example, a statement such as "following the experiment, a 95% credible interval for the parameter t is 35-45" means that the posterior probability that t lies in the interval from 35 to 45 is 0.9.

A Bayesian credible interval incorporates information from the prior distribution into the estimate, while confidence intervals are based solely on the data.

Like 'confidence interval' vs 'credible interval, there is also 'confidence region' vs 'credible region'.

Here are some links for further reading:

• Credible interval at wikepedia
• Bland and Altman (1998) Bayesians and frequentists. BMJ
• Fisher (1996) Comments on Bayesian and Frequentist Analysis and Interpretation of Clinical Trials. Controlled Clinical Trials
• Credible Interval
• Credible Intervals vs. Confidence Intervals

Placebo and Sham treatment: are they really inactive?

According the ICH guidance E10 (CHOICE OF CONTROL GROUP AND RELATED ISSUES IN CLINICAL TRIALS), "A placebo is a "dummy" treatment that appears as identical as possible to the test treatment with respect to physical characteristics such as color, weight, taste and smell, but that does not contain the test drug."

We typically use the term Placebo, but sometime, the term 'sham treatment' is used. The word 'sham' means something that is a fake or an imitation that purports to be genuine.

In practice, a placebo is often defined as an inactive substance made to appear like a medication or a sham procedure or device imitating a known treatment. Sometimes, the 'inactive' substance used in the clinical trial may not be totally 'inactive'. One example is albumin. On the one hand, the albumin may be treated as inactive substance for Placebo; on the other hand, there are studies to study the effect of albumin in certain diseases. In a study about "the Effectiveness of Intravenous Immune Globulin (10%) for the Treatment of Multifocal Motor Neuropathy", 0.25% human albumin solution was used as Placebo. But there are also plenty of clinical trials to study the efficacy of albumin in sepsis, renal impairment, acute stroke,...

In a lot of publications, the author did not disclose what the placebo is. You can use the same term 'placebo', but the 'placebo' could be sugar pill, saline, albumin,...

Even more...

In article web article by BJ Appelgren titled "The Placebo as Medicine Viewed as Sham, Placebo Itself May Be the Most Significant", the following examples are cited as other type of placebos.

• Having an interaction with a health care provider
• The presence of something symbolic in the encounter such as contact with a person wearing a “white coat,” perceived as a provider of healing

The significance of symbols cannot be measured objectively and, for that reason, is not valued. Researchers also have an additional puzzle when non-treatment causes positive results. Too often, when the effect of symbolism is recognized by conventional medicine, it is removed from a context of positive meaning and denigrated as “being all in the mind,” as if that makes it illusory.

SAS IQ and OQ

I am not sure how many people really know these abbreviations: DOE, IQ, OQ, PQ, PV. These are the terms used in the validation of a software or computerized systems.

DOE = Design of Experiment
IQ = Installation Qualification
OQ = Operational Qualification
PQ = Performance Qualification
PV = Process Validation

For off-the-shelf software, I have never really thought about the validation or qualification issue. I always think that the software like SAS (we use it almost daily) is just like the Miscrosoft Office. Once you install on your PC, you are ready to use.

I really learned that if the software is used for regulatory submission, certain level of validation (precisely qualification) need to be performed. There is no exception for SAS.

For SAS software, the IQ and OQ need to be performed. The instructions for the SASInstallation Qualification (IQ) and Operational Qualification (OQ) tools can be found at SAS website and at http://support.sas.com/kb/17/046.html. This was also mentioned in SAS quality document. SAS actually has a SOP for IQ and OC.

By digging in this issue further, the verification and validation of a software or computerized system is not a trivial task. Wikipedia has a topic discussing about verification and validation. The recent issue of DIA Global forum has an article by Chamberlain and they discussed qualification (vs validation) of the infrastructure.

However, I think that the validation for off-the-shelf software should be much simpler than a self-developed computerized system (such as an internal EDC system). FDA has a pertinent guidance about the computerized systems: Computerized systems used in clinical investigations and its old version titled "Computerized systems used in clinical trials".

CDRH also had a guidance titled "General Principles of Software Validation; Final Guidance for
Industry and FDA Staff". This guidance indicated that the software used in medical device need to go through a full-scale validation process.

Hochberg procedure for adjustment for multiplicity - an illustration

In a May article, I discussed several practical procedures for multiple testing issue. One of the procedures is Hockberg's procedure. The original paper is pretty short and published in Biometrika.

Hochberg (1988) A sharper Bonferroni procedure for multiple tests of significance. Biometrika 75(4):800-802

Hochberg's procedure is a step-up procedure and its comparison with other procedures are discussed in a paper by Huang & Hsu.

To help the non-statisticians to understand the application of Hochberg's procedure, we can use the hypothetical examples (three situations with three pairs of p-values).

Suppose we have k=2 t-tests
Assume target alpha(T)=0.05

Unadjusted p-values are ordered from the largest to the smallest

Situation #1:
P1=0.074
P2=0.013

For the jth test, calculate alpha(j) = alpha(T)/(k – j +1)

For test j = 2,
alpha(j) = alpha(T)/(k – j +1)
= 0.05/(2 – 2 + 1)
= 0.05

P1=0.074 is greater than 0.05, we can not reject the null hypothesis. Proceed to the next test

For test j = 1,
alpha(j) = alpha(T)/(k – j +1)
= 0.05/(2 – 1 + 1)
= 0.025

P2=0.013 is less than 0.025, reject the null hypothesis.

Situation #2:
P1=0.074
P2=0.030
For the jth test, calculate alpha(j) = alpha(T)/(k – j +1)

For test j = 2,
alpha(j) = alpha(T)/(k – j +1)
= 0.05/(2 – 2 + 1)
= 0.05

P1=0.074 is greater than 0.05, we can not reject the null hypothesis. Proceed to the next test

For test j = 1,
alpha(j) = alpha(T)/(k – j +1)
= 0.05/(2 – 1 + 1)
= 0.025

P2=0.030 is greater than 0.025, we can not reject the null hypothesis.

Situation #3:
P1=0.013
P2=0.001
For the jth test, calculate alpha(j) = alpha(T)/(k – j +1)

For test j = 2,
alpha(j) = alpha(T)/(k – j +1)
= 0.05/(2 – 2 + 1)
= 0.05

P1=0.013 is less than 0.05, we reject the null hypothesis.
Since the all p-values are less than 0.05, we reject all null hypothesis at 0,05.

More than two comparisons
If we have more than two comparisons, we can still use the same logic

For the jth test, calculate alpha(j) = alpha(T)/(k – j +1)

For example, if there are three comparisons with p-values as:
p1=0.074
p2=0.013
p3=0.010

For test j = 3,
alpha(j) = alpha(T)/(k – j +1)
= 0.05/(3 – 3 + 1)
= 0.05

For test j=3, the observed p1 = 0.074 is less than alpha(j) = 0.05, so we can not reject the null hypothesis. We proceed to the next test.


For test j = 2,
alpha(j) = alpha(T)/(k – j +1)
= 0.05/(3 – 2 + 1)
= 0.05 / 2
= 0.025

For test j=2, the observed p2 = 0.013 is less than alpha(j) = 0.025, so we reject all remaining null hypothesis.



For example, if there are three comparisons with p-values as:
p1=0.074
p2=0.030
p3=0.010

For test j = 3,
alpha(j) = alpha(T)/(k – j +1)
= 0.05/(3 – 3 + 1)
= 0.05

For test j=3, the observed p1 = 0.074 is less than alpha(j) = 0.05, so we can not reject the null hypothesis. We proceed to the next test.


For test j = 2,
alpha(j) = alpha(T)/(k – j +1)
= 0.05/(3 – 2 + 1)
= 0.05 / 2
= 0.025

For test j=2, the observed p2 = 0.030 is greater than alpha(j) = 0.025, so we can not reject the null hypothesis. We proceed to the next test.

For test j = 1,
alpha(j) = alpha(T)/(k – j +1)
= 0.05/(3 – 1 + 1)
= 0.05 / 3
= 0.017

For test j=2, the observed p2 = 0.010 is less than alpha(j) = 0.017, so we can reject the null hypothesis.
.

Poisson regression and zero-inflated Poisson regression

Poisson regression is a method to model the frequency of event counts or the event rate, such as the number of adverse events of a certain type or frequency of epileptic seizures during a clinical trial, by a set of covariates. The counts are assumed to follow a Poisson distribution with other variables that are modeled as a function of the covariates. The Poisson regression model is a special case of a generalized linear model (GLM) with a log link - this is why the Poisson regression may also be called Log-Linear Model . Consequently, it is often presented as an example in the broader context of GLM theory.

Poisson regression is the simplest regression model for count data and assumes that each observed count Yi is drawn from a Poisson distribution with the conditional mean ui on a given vector Xi for case i. The number of events follows the Poisson distribution that is described blow:

where

• e is the base of the natural logarithm (e = 2.71828...)
• k is the number of occurrences of an event - the probability of which is given by the function
• k! is the factorial of k
• λ is a positive real number, equal to the expected number of occurrences that occur during the given interval, the interval could be a time interval or other offset variables (denominators).

The most important feature of the Poisson regressin is that the parameter λ is not only the mean number of occurrences, but also its variance. In other words, to follow the Poisson distribution, the mean equals to the variance. However, with the empirical data (observations), this feature may not always fit - a situation called overdisperse or underdisperse. When the observed variance is higher than the variance of a theoretical model (or for Poisson distribution, the observed variance is higher than the observed mean), overdispersion has occurred. Conversely, underdispersion means that there was less variation in the data than predicted.

When overdisperse occurs, an alternative model with additional free parameters may provide a better fit. In the case of the count data, an alternaitve model such as negative binomial distribution may be used.

In practice, we often see the count data with excessive zero counts (no event), which may cause the deviation from the Poisson distribution - overdispersion or underdispersion. If this is the case, zero-inflated Poisson regression may be used.

In SAS, several procedures in both STAT and ETS modules can be used to estimate Poisson regression. While GENMOD, GLIMMIX (from SAS/Stat), and COUNTREG (from SAS/ETS) are easy to use with standard MODEL statement, NLMIXED, MODEL, NLIN provide great flexibility to model count data by specifying the log likelihood function explicitly.

• Excellent Discussion about Zero-Inflated Poisson Regression by UCLA Academic Technology Services
• Count Data Model using SAS by Liu and Cela
• Zero-Inflated Poisson and Zero-Inflated Negative Binomial Models Using the COUNTREG Procedure by Erdman et al
• Design and Analysis of Count Data by Lakshminarayanan
• Proc Countreg user's guide from SAS
• Course notes about negative binomial distribution by Dr.Preisser in UNC
  
  

Epidemiology terms, but used in clinical trials

Some terms often used in epidemiology fields are actually pretty commonly used in clinical trials. At least for me, I first learned these terms in epidemiology classes. Some of these terms are very close, but different.

Ratio, Proportion, Rate

• Ratio: Division of two unrelated numbers
• Proportion: Division of two related numbers; numerator is a subset of denominator
• Rate: Division of two numbers; time is always in denominator

For example, 'sex ratio' is a ratio (the number of males divided by the number of females). Rising sex-ratio imbalance is a danger in China.
In a clinical trial, there are males subjects and female subjects. We summarized the data using the percentage of male subjects among the total - this is proportion. The # of male subjects (numerator) is a subset of the total subjects (denominator).
A rate is also one number divided by another, but time is an integral part of the denominator. For example, the speed limit is a rate (65 miles per hour). In clinical trial, rate is often used to describe the incidence of adverse events.

Incidence and prevalence

• Incidence: measures the occurrence of new disease; deals with the transition from health to disease; defined as the occurrence of new cases of disease that develop in a candidate population over a specified time period
• Prevalence: measures the existence of current disease; focuses on the period of time that a person lives with a disease; measures the frequency with which new disease develops; defined as the proportion of the total population that is diseased.
  

Incidence is typically used for describing the acute disease while the prevalence is typically used for describing the chronic disease.

Both incidence and prevalence are rate, not ratio, not proportion. In practice, it comes the terms such as incidence rate and prevalence rate.

While prevalence is purely an epidemiology term, 'incidence' or 'incidence rate' is commonly used in the analysis of clinical trial data, especially the adverse event data. Clinical trial design is always prospective and can be considered as a special case of cohort study in epidemiology term.
In statistics and demography, a cohort is a group of subjects who have shared a particular experience during a particular time span. Cohorts may be tracked over extended periods of time in a cohort study. Notice that we also use the term 'cohort' in dose-escalation clinical studies where the cohort refers to a group of subjects who receive the same level of dose (this is contrary to the term 'arm' used in parallel design).

Incidence vs. Incidence Rate

In clinical trial, when we summarize the adverse event data, should we say "incidence of adverse events" or "incidence rate of adverse events"?

While both terms may be used, "incidence of adverse events" should be more accurate and is more frequently used. This can be easily seen in FDA guidance documents, for example:

• Formatting of Bioequivalence Summary Tables
• Guidance on Immune Globulin Intravenous (Human) as Replacement Therapy for Primary Humoral Immunodeficiency
• Guidance on FDA’s Transition Plan for Existing Postmarket Surveillance Protocols
  

"Incidence rate" may be more appropriate when the # of adverse events are normalized by the person year or patient year or normalized by the # of infusions, for example, the following terms may be used: "incidence rate of adverse events per infusion" "The incidence rates per 100 patients-year"

Some axiom quotes about statistics

I had a chance to listen to a seminar by Richard De Veaux in an event organized by SAS JMP for data mining. Dick is really an excellent speaker/tutor. He can make the complex / boring statistical issues sound easy and interesting. One thing I noticed is that he used some interesting axiom quotes and catoons about the statistics. Here are some quotes he used in his talk.

George Box:

• “All models are wrong, but some are useful”
• “Statisticians, like artists, have the bad habit of falling in love with their models”.

Twyman’s Law and Corollaries

• “If it looks interesting, it must be wrong”
• De Veaux’s Corollary 1 to Twyman’s Law: “If it’s perfect, it’s wrong”
• De Veaux’s Corollary 2 to Twyman’s Law: “If it isn’t wrong, you probably knew it already

Albert Einstein:
"All models should be as simple as possible but no simpler than necessary"
......

By simply googling the website, I can find some additional quotes/axioms:
David Hand:

• “Data mining is the discovery of interesting, unexpected, or valuable structures in large datasets”

Twyman's Law:

• "If it’s interesting or unusual it’s probably wrong"

Geroge Box:

• “All models are wrong, some are useful”

Unknown source:

• “If we torture the data long enough, they will confess”
• "What’s the difference between a biostatistician and a physician? A physician makes an analysis of a complex illness whereas a biostatistician makes you ill with a complex analysis."

Further about Twyman's law:
Twyman's Law (created by Tony Twyman the expert UK based media analyst) states that "If a thing surprises you, it's wrong" Has anyone investigated to what extent the reported loss is real or a research arifact?

There is a rule in market research called Twyman’s law: “anything surprising or interesting is probably wrong”. While not going that far, one should be always advised that if you find a poll result that seems somewhat counter-intuitive, that seems to have no obvious explanation, treat it with caution until other polls support the findings. Statistically there is no more reason for this poll to be wrong than the last poll or the poll before that, and we may indeed find that this is a genuine trend and everyone starts showing the Tories down, but it is a bit odd.


Jim's favorite quotes
Statistics Catoons
Imaging results about catoon statistics from google
Use humor to teach statistics
Collection of statistics joke and humor

Dose Escalation and Modified Fabonacci Series

Dose-escalation is a type of clinical trial design in which the amount of the drug is increased with each cohort that is added. Each cohort is called 'dose cohort' and the size of each cohort could be different depending on the nature of the study. Typically the cohort size is around 10 subjects. Dose-escalation study design is used to determine how a drug is tolerated in people and it is often used in first-in-men trial. In dose escalation study, a new cohort should not be initiated before safety data in the current or previous cohort has been fully assessed. Sometimes, it may be useful to pre-define a safety stopping rule to prevent the increase of the dose cohort if something bad happens.

One thing for a dose escalation study is how to determine the dose space (ie, how much increase in terms of the dose comparing with the previous cohort). One schema to determine the dose space is so called 'Modified Fabonacci Series'.

In the 12th century, Leonardo Fibonacci discovered a simple numerical series that is the foundation for an incredible mathematical relationship behind phi.

Starting with 0 and 1, each new number in the series is simply the sum of the two before it.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . . .

The ratios of the successive numbers in the Fibonacci series quickly converge on Phi. After the 40th number in the series, the ratio is accurate to 15 decimal places.

1.618033988749895 . . .

A “modified” Fibonacci series uses starting numbers other than 0 and 1. For example, the starting number is 1 and 3, we will have a modified Fibonacci series as following:

1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843, 1364, 2207, 3571, 5778, 9349...

The modified Fibonacci series has been used in Phase I dose escalation study to determine the dose space.

Assuming the d1 is the starting dose for the first cohort, according to the modified Fabonacci series, the next dose cohort will be d2=2d1, and then d3=1.67d2, d4=1.5d3,... If the start dose is 5 mg and a study with 5 cohorts, the dose schema will be:

Cohort 1 (5 mg) -> Cohort 2 (10 mg) -> Cohort 3 (15 mg) -> Cohort 4 (25 mg) -> Cohort 5 (40 mg)

As we can see, with the dose increase, the ratio between two consecutive doses are getting smaller and smaller.

Further reading on the modified Fabonacci series and its application in dose escalation studies:

• Christophe Le Tourneau, J. Jack Lee, Lillian L. Siu (2009 JNCI) Dose Escalation Methods in Phase I Cancer Clinical Trials
• Phase I Clinical Trial Design by Lawrence V Rubinstein and Richard M Simon
• George Omura (2003) Modified Fibonacci Search Journal of Clinical Oncology

Odds Ratio and Relative Risk

Odds Ratio (OR) and Relative Risk (RR) are two ratios often used in the epidemiology studies and the clinical trials. They are related, but the calculation and the interpretation are quite different. Notice that the Relative Risk (RR) may also be called Risk Ratio with the same abbreviation of RR.

Relative Risk

P0=The probability of events (eg., responder, cardiovascular event) when a covaraite is at a give level (eg, treatment = Placebo, gender=female)
P1=The probability of events (eg., responder, cardiovascular event) when a covariate is at one unit higher than the previous level (eg., treatment = New Drug) or simply another level (gender=male)
RR = P1 / P0

Odds Ratio
Odds = The probability of events / the probablity of non-events
OR = Odds in one group / odds in another group = P1/((1-P1) divided by P0/(1-P0)
For example, OR = Odds in treated group / Odds in Placebo group

When P1 and P0 are small, OR can be used to estimate RR. However, then P1 and P0 are close to 0.5, the OR is typically much larger than RR.

Steve Simon wrote an excellent web page about the comparison of Odds Ratio versus Relative Risk.

In epidemiology class, we are typically advised to use OR for case-control study and use RR for cohort study. For cross-section studies, both OR and RR may be used.

In clinical trial setting, there is no consensus of using OR or RR. In practice, both of them are used. Sometimes, using OR or RR could be manipulated to serve one purpose or another. Brian Attig and Alison Clabaugh criticized the misuse of statistical interpretation of the odds ratio in APPLIED CLINICAL TRIALS.

Both OR and RR can be easily obtained from SAS Proc Freq with RISKDIFF option. An example by Mimi Chong from the following website illustrates this. We just need to be careful when we read the results from the SAS outputs. Odds ratio is clearly labelled and the Risk ratio is the the numbers corresponding to 'Col1 Risk' or 'col 2 risk' depending on which column is defined as 'event'.

If additional covariates (or in epimiology term, confounding factors) need to be considered, SAS Proc Freq with CMH option or Proc Logistic regression or Proc Genmod can be used.

The interactive voice response system

Interactive Voice Response (IVR) is an interactive technology that allows a computer to detect voice and keypad inputs. Its use in clinical trial probably started with the randomization. It replaces the old way in handling the randomization (i.e., through concealed envelopes). It makes the central randomization feasible and make it easy for handling the complex randomization schedules such as the randomization with multiple layers of stratefications and the randomization with dynamic allocation.


Currently most sponsors perform randomization using an Interactive Voice Response System (IVRS) so that treatment codes for individual patients are no longer available at the sites for inspection.


The IVRS utilizes a dynamic randomization system using an adaptive minimization technique for pre-specified stratification variables. The randomization algorithm evaluates previous treatment assignments across the different strata to determine the probability of treatment assignment. There are no fixed randomization lists available prior to enrollment of patients and there are no pre-determined randomization schedules. The randomization algorithm is the source document and is supposed to be signed and dated prior to the time when the first patient is randomized into the study. An external vendor is used to manage the treatment allocation codes. Once a subject is found to be eligible for a trial, the investigator contacts the IVRS vendor and provides details about the subject including their stratification factors. Typically sites receive confirmation faxes from the IVRS vendor that include relevant patient information such as the date of randomization, the date of last visit and the date the last medication was assigned.


In emergences, investigators must call the IVRS vendor to break the treatment code since there are no longer envelopes with patient numbers and treatment codes for investigators to open at the sites. Treatment codes may be released to external vendors prior to the final analysis in order for plasma concentration analyses or PK modeling to be performed in patients receiving the new investigational treatment. Treatment codes may also be released or partially broken up to the code level (e.g. treatment A, B) for the Data Safety Monitoring Board (DSMB) and may be completely unblinded if the chairman of the DSMB requests it. Treatment codes are released to the sponsor or contract research organization after the official analysis database lock.



Nowadays, the IVRS moves to the web-based system. The term is also becoming IWRS (interactive web response system). It could be the situation, when we use the term IVRS, it actually means IWRS.



The utility of the IVRS/IWRS is not just limited to the randomization. It can be used in other areas as well:

• Collecting the clinical efficacy outcome. For example, in IBS (Irritable Bowel Syndrome) study, the IVRS is used to collect the information about the presence or intensity of several IBS related symptoms daily (such as satisfactory relief, Abdominal discomfort or pain, Bloating, Stool frequency, Stool consistency...)
• Patient Reported Outcome (ePRO)
• Outcome research
• Cohort management (open/close a cohort) in dose-escalation studies
• Patient registry / registry studies
• Drug supply managment / Study drug inventory tracking

Spaghetti Plot

The first time when I used the term "Spaghetti" was for one of the pharmacokinetic studies where I would like to see the time-concentration curves for all individuals plotted on the same panel. The figure on the right side is an example of a Spaghetti plot from simulated data.

I don't think there is any formal definition for Spaghetti Plot, but this term refers to the plot for visualizing the trajectories for all individual subjects. The name “spaghetti plot” is called because it looks a bit like spaghetti noodles thrown on a wall.



The funny thing is that one time when I used the term 'spaghetti plot', I was asked not to use this term since it sounded like 'not formal'. Instead of using 'spaghetti plot', I had to change it to 'indivudual plots' or something like that. As a matter of fact, this term is actually used pretty often in pharmacokinetic studies and also in longitudinal studies.

In longitudinal studies, the spaghetti plot is used to visualize the trajectories or patterns or time trends. The spaghetti plot is typically used in the situation that the # of subjects is not too large and is generated for each group (if there is two treatment groups, there will be one spaghetti plot for each treatment group).

Spaghetti plot can be easily generated by software such as R and SAS. In SAS, the following statement can be used:

symbol1 value = circle color = black interpol = join repeat = 5;
proc gplot;
plot y*time = id / nolegend;
run;

Where y is the desired variable we would like to visualize; time is the time or visit; id is the subject #.

Some further readings:
1. UCLA: How can I visualize longitudinal data in SAS?
2. A oral contraceptive drug interaction study
3. A lecture notes by derived variable summaries
4. Quantitative Methods for Tracking Cognitive Change 3 Years After CABG

Williams Design

Williams Design is a special case of orthogonal latin squares design. It is a high-crossover design and typically used in Phase I studies. Due to the limitation of the # of subjects, we would like to achieve the balance and maximize the comparisons with the smallest # of subjects.

A Williams design possesses balance property and requires fewer sequences and periods. If the number of treatments (n) is an odd number, there will be 2 x n number of sequences. If the number of treatments (n) is an even number, there will be n number of sequences. The example below is a Williams Design with a 4 by 4 crossover (four treatments, four sequences, and also four periods).

Let A, B, C, and D stand for four different treatments, a Williams Design will be arranged as:

A D B C
B A C D
C B D A
D C A B

Notice that each treatment only occurs one time in one sequence, in one period. Furthermore, each treatment only follow another treatment one time. For example, treatment D following treatment B only one time in all sequences.

Several years ago, I wrote a paper on generating the randomization schedule using SAS. I illustrated an example for Williams Design.

There is a new paper by Wang et al specifically discussing about "The Construction of a Williams Design and Randomization in Cross-Over Clinical Trials using SAS"

Williams Design is deliberated in detail in the books "Design and Analysis of Clinical Trials" and Design and Analysis of Bioavailability and Bioequivalence Studies" by Chow and Liu

Williams Design is not purely used in Phase I or bioavailabity studies. I participated in a study with drug abuse area where a Williams design was used. It looks like that other people also uses Williams Design in drug abuse research.

Protocol Amendment after IND

In clinical development, filing of IND (Investigational New Drug) is an important milestone. FDA is required by the Modernization Act to respond in writing to an IND sponsor within 30 calendar days of receipt of the sponsor’s IND filing including the clinical study protocol(s). If the clinical study is not put on hold, the sponsor can start all clinical work including the patient enrollment.

After the initial IND is approved, how to oversee the IND if the sponsor makes significant changes to the study protocol?

First of all, any changes in the research protocol (protocol amendment or administrative letter) or patient informed consent form must be approved by the IRB (institutional Review Board) before the investigator or any sub-investigators put those changes into effect

Secondly, the protocol amendment needs to be submitted to FDA (immediately or through IND annual report). According to 21CFR312.30, the following requirements are stated:

"(b) Changes in a protocol. (1) A sponsor shall submit a protocol

amendment describing any change in a Phase 1 protocol that significantly
affects the safety of subjects or any change in a Phase 2 or 3 protocol
that significantly affects the safety of subjects, the scope of the
investigation, or the scientific quality of the study. Examples of
changes requiring an amendment under this paragraph include:
 (i) Any increase in drug dosage or duration of exposure of
individual subjects to the drug beyond that in the current protocol, or
any significant increase in the number of subjects under study.
 (ii) Any significant change in the design of a protocol (such as the
addition or dropping of a control group).
 (iii) The addition of a new test or procedure that is intended to
improve monitoring for, or reduce the risk of, a side effect or adverse
event; or the dropping of a test intended to monitor safety.
 (2)(i) A protocol change under paragraph (b)(1) of this section may
be made provided two conditions are met:
 (a) The sponsor has submitted the change to FDA for its review; and
 (b) The change has been approved by the IRB with responsibility for
review and approval of the study. The sponsor may comply with these two
conditions in either order.
 (ii) Notwithstanding paragraph (b)(2)(i) of this section, a protocol
change intended to eliminate an apparent immediate hazard to subjects
may be implemented immediately provided FDA is subsequently notified by
protocol amendment and the reviewing IRB is notified in accordance with
Sec. 56.104(c)."

IN FDA's compliance program guidance manual on 'clinical investigators and sponsor investigators', 

there are the following statements:

"Protocol changes/amendments. During the course of a study, a protocol may be formally changed 

by the sponsor. Such a change is usually prospectively planned and implemented in a systematic 

fashion through a protocol amendment. Protocol amendments must be reviewed and approved by 

the IRB, prior to implementation, and submitted to FDA. "

Not all protocol changes require the submission of a formal protocol amendment,
however, the sponsor's reporting responsibility depends on the nature of the
change.  In practice, many companies adopt a conservative approach by reporting
virtually all protocol changes.

Double Dummy Technique

Double dummy is a technique for retaining the blind when administering supplies in a clinical trial, when the two treatments cannot be made identical. Supplies are prepared for Treatment A (active and indistinguishable placebo) and for Treatment B (active and indistinguishable placebo). Subjects then take two sets of treatment; either A (active) and B (placebo), or A (placebo) and B (active).

Double dummy is a method of blinding where both treatment groups may receive placebo. For example, one group may receive Treatment A and the placebo of Treatment B; the other group would receive Treatment B and the placebo of Treatment A.

The figure on the left side is a double-dummy example for a two treatmetn arm scenario. The figure on the right side is a double-dummy example for a three-arm scenario. To maintain the blinding, subjects in each arm will take one tablet and one capsule. In the example on the right side table, subject in placebo arm will take one placebo tablet and one placebo capsule.

Group t-test or Chi-square test based on the summary data

Sometimes, the only data we have is the summary data (mean, standard deviation, # of subjects). Can we use the summary data (instead of the raw data) to calculate the statistical and p-values?

Yes, we can.

Below is an example for group t-test. I illustrate two methods for calculating the p-values based on the summary data.

In the method 1, we will use the SAS procedure PROC TTEST. The only trick thing is to enter the summary data in a data set with an SAS internal variable _STAT_ for the indicator of the summary statistics. The program below is self-explanatory.

data summary;
length _stat_ $4;
input week $ _STAT_ $ value@@;
datalines;
w1 n 7
w1 mean -2.6
w1 std 1.13
w2 n 5
w2 mean -1.2
w2 std 0.45
;
proc print;run;
proc ttest data=summary;
class week;
var value;
run;


Another way is to use the formula.


The correct formula for calculating the t value for group t-test is shown on the right side Where m=0 with degree freedom of n1+n2-2. To compare means from two independent samples with n1 and n2 observations to a value m, this formula can also be used.

where s**2 is the pooled variance

s**2 = [((n1-1)s1**2+(n2-1)s2**2)/(n1+n2-2)]

and s1**2 and s2**2 are the sample variances of the two groups. The use of this t statistic depends on the assumption that sigma1**2=sigma2**2, where sigma1**2 and sigma2**2 are the population variances of the two groups.

*Method #2;
data ttest;
input n1 mean1 sd1 n2 mean2 sd2;
s2 = (((n1-1)*sd1**2+(n2-1)*sd2**2)/(n1+n2-2));
s =sqrt(s2);
denominator = s * sqrt((1/n1) + (1/n2));
df = n1+n2-2;
t = (mean1 - mean2)/denominator;
p = (1-probt(abs(t),df))*2;
datalines;
7 -2.6 1.13
5 -1.2 0.45
;
run;
proc print;
run;

It will be even easier if the summary data is # of counts or frequency data. we can use SAS PROC FREQ option WEIGHT to indicate that data is for # of counts instead of the original individual data. The SAS codes will be something like:

data disease;
do exposure=1 to 2;
do disease=1 to 2;
input index@;
output;
end;
end;
cards;
23 32
17 15
;
proc freq data=disease;
tables exposure*disease/chisq;
weight index;
run;

Pharmacokinetics: Verify the Steady State Under Multiple Doses

For a multiple-dose regimen, the amount of drug in the body is said to have reached a steady state level if the amount or average concentration of the drug in the body remains stable. At steady state, the rate of elimination = the rate of administration.

To determine whether the steady state is achieved, statistical test can be performed on the trough levels. The predose blood sampling should include at least three successive trough level samples (Cmin).

In FDA's guidance for industry: Bioequivalence Guidance, it stated "...to determine a steady state concentration, the Cmin values should be regressed over time and the resultant slope should be tested for its difference from zero." For example, we can use the logarithm of last three trough measurements to regress over time. If the 90% CI for the exponential of slope for time is within (0.9, 1.1), then we will claim SS. The limit of (0.9, 1.1) is arbitrarily decided.


Similarly, in FDA's guidance for Industry: Clozapine Tablets: In Vivo Bioequivalence and In Vitro Dissolution Testing, it stated "...The trough concentration data should also be analyzed statistically to verify that steady-state was achieved prior to Period 1 and Period 2 pharmacokinetic sampling."

Typically, the verification of the steady state can simply be the review of the trough levels at time points prior to the PK sampling without formal statistical testing. If the PK blood samples are taken after 4-5 dose intervals, it can be roughly assumed that the (approximately or near) steady state has been reached.
The trough and peak values of plasma concentrations are also used to determine whether the steady state has been reached. The peak to trough ratio is usually used as an indicator of fluctuation of drug efficacy and safety. A relatively small peak to trough ratio indicates that the study drug is relatively effective and safe.

In their book "Design and analysis of bioavailability and bioequivalence studies", Chow and Liu described the univariate analysis and multivariate anaysis approaches to test the steady state formally.

Hong also proposed a non-linear procedure to test for steady state.

A note about trough and Cmin:

The characteristic Cmin has been associated with the concentration at the end of te dosing interval, the so-called pre-dose or trough value. However, for prolonged release formulations which exhibit an apparent lag-time of absorption, the true minimum (trough) concentration may be observed some time after the next dosing, but not necessarily at the end of the previous dosing interval.