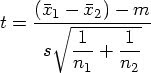In a May article, I discussed several
practical procedures for multiple testing issue. One of the procedures is Hockberg's procedure. The original paper is pretty short and published in Biometrika.
Hochberg (1988) A sharper Bonferroni procedure for multiple tests of significance. Biometrika 75(4):800-802
Hochberg's procedure is a step-up procedure and its comparison with other procedures are discussed in
a paper by Huang & Hsu.
To help the non-statisticians to understand the application of Hochberg's procedure, we can use the hypothetical examples (three situations with three pairs of p-values).
Suppose we have k=2 t-tests
Assume target alpha(T)=0.05
Unadjusted p-values are ordered from the largest to the smallest
Situation #1:
P1=0.074
P2=0.013
For the jth test, calculate alpha(j) = alpha(T)/(k – j +1)
For test j = 2,
alpha(j) = alpha(T)/(k – j +1)
= 0.05/(2 – 2 + 1)
= 0.05
P1=0.074 is greater than 0.05, we can not reject the null hypothesis. Proceed to the next test
For test j = 1,
alpha(j) = alpha(T)/(k – j +1)
= 0.05/(2 – 1 + 1)
= 0.025
P2=0.013 is less than 0.025, reject the null hypothesis.
Situation #2:
P1=0.074
P2=0.030
For the jth test, calculate alpha(j) = alpha(T)/(k – j +1)
For test j = 2,
alpha(j) = alpha(T)/(k – j +1)
= 0.05/(2 – 2 + 1)
= 0.05
P1=0.074 is greater than 0.05, we can not reject the null hypothesis. Proceed to the next test
For test j = 1,
alpha(j) = alpha(T)/(k – j +1)
= 0.05/(2 – 1 + 1)
= 0.025
P2=0.030 is greater than 0.025, we can not reject the null hypothesis.
Situation #3:
P1=0.013
P2=0.001
For the jth test, calculate alpha(j) = alpha(T)/(k – j +1)
For test j = 2,
alpha(j) = alpha(T)/(k – j +1)
= 0.05/(2 – 2 + 1)
= 0.05
P1=0.013 is less than 0.05, we reject the null hypothesis.
Since the all p-values are less than 0.05, we reject all null hypothesis at 0,05.
More than two comparisons
If we have more than two comparisons, we can still use the same logic
For the jth test, calculate alpha(j) = alpha(T)/(k – j +1)
For example, if there are three comparisons with p-values as:
p1=0.074
p2=0.013
p3=0.010
For test j = 3,
alpha(j) = alpha(T)/(k – j +1)
= 0.05/(3 – 3 + 1)
= 0.05
For test j=3, the observed p1 = 0.074 is less than alpha(j) = 0.05, so we can not reject the null hypothesis. We proceed to the next test.
For test j = 2,
alpha(j) = alpha(T)/(k – j +1)
= 0.05/(3 – 2 + 1)
= 0.05 / 2
= 0.025
For test j=2, the observed p2 = 0.013 is less than alpha(j) = 0.025, so we reject all remaining null hypothesis.
For example, if there are three comparisons with p-values as:
p1=0.074
p2=0.030
p3=0.010
For test j = 3,
alpha(j) = alpha(T)/(k – j +1)
= 0.05/(3 – 3 + 1)
= 0.05
For test j=3, the observed p1 = 0.074 is less than alpha(j) = 0.05, so we can not reject the null hypothesis. We proceed to the next test.
For test j = 2,
alpha(j) = alpha(T)/(k – j +1)
= 0.05/(3 – 2 + 1)
= 0.05 / 2
= 0.025
For test j=2, the observed p2 = 0.030 is greater than alpha(j) = 0.025, so we can not reject the null hypothesis. We proceed to the next test.
For test j = 1,
alpha(j) = alpha(T)/(k – j +1)
= 0.05/(3 – 1 + 1)
= 0.05 / 3
= 0.017
For test j=2, the observed p2 = 0.010 is less than alpha(j) = 0.017, so we can reject the null hypothesis.
.