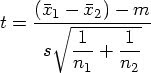Some axiom quotes about statistics

I had a chance to listen to a seminar by Richard De Veaux in an event organized by SAS JMP for data mining. Dick is really an excellent speaker/tutor. He can make the complex / boring statistical issues sound easy and interesting. One thing I noticed is that he used some interesting axiom quotes and catoons about the statistics. Here are some quotes he used in his talk.

George Box:

• “All models are wrong, but some are useful”
• “Statisticians, like artists, have the bad habit of falling in love with their models”.

Twyman’s Law and Corollaries

• “If it looks interesting, it must be wrong”
• De Veaux’s Corollary 1 to Twyman’s Law: “If it’s perfect, it’s wrong”
• De Veaux’s Corollary 2 to Twyman’s Law: “If it isn’t wrong, you probably knew it already

Albert Einstein:
"All models should be as simple as possible but no simpler than necessary"
......

By simply googling the website, I can find some additional quotes/axioms:
David Hand:

• “Data mining is the discovery of interesting, unexpected, or valuable structures in large datasets”

Twyman's Law:

• "If it’s interesting or unusual it’s probably wrong"

Geroge Box:

• “All models are wrong, some are useful”

Unknown source:

• “If we torture the data long enough, they will confess”
• "What’s the difference between a biostatistician and a physician? A physician makes an analysis of a complex illness whereas a biostatistician makes you ill with a complex analysis."

Further about Twyman's law:
Twyman's Law (created by Tony Twyman the expert UK based media analyst) states that "If a thing surprises you, it's wrong" Has anyone investigated to what extent the reported loss is real or a research arifact?

There is a rule in market research called Twyman’s law: “anything surprising or interesting is probably wrong”. While not going that far, one should be always advised that if you find a poll result that seems somewhat counter-intuitive, that seems to have no obvious explanation, treat it with caution until other polls support the findings. Statistically there is no more reason for this poll to be wrong than the last poll or the poll before that, and we may indeed find that this is a genuine trend and everyone starts showing the Tories down, but it is a bit odd.


Jim's favorite quotes
Statistics Catoons
Imaging results about catoon statistics from google
Use humor to teach statistics
Collection of statistics joke and humor

Dose Escalation and Modified Fabonacci Series

Dose-escalation is a type of clinical trial design in which the amount of the drug is increased with each cohort that is added. Each cohort is called 'dose cohort' and the size of each cohort could be different depending on the nature of the study. Typically the cohort size is around 10 subjects. Dose-escalation study design is used to determine how a drug is tolerated in people and it is often used in first-in-men trial. In dose escalation study, a new cohort should not be initiated before safety data in the current or previous cohort has been fully assessed. Sometimes, it may be useful to pre-define a safety stopping rule to prevent the increase of the dose cohort if something bad happens.

One thing for a dose escalation study is how to determine the dose space (ie, how much increase in terms of the dose comparing with the previous cohort). One schema to determine the dose space is so called 'Modified Fabonacci Series'.

In the 12th century, Leonardo Fibonacci discovered a simple numerical series that is the foundation for an incredible mathematical relationship behind phi.

Starting with 0 and 1, each new number in the series is simply the sum of the two before it.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . . .

The ratios of the successive numbers in the Fibonacci series quickly converge on Phi. After the 40th number in the series, the ratio is accurate to 15 decimal places.

1.618033988749895 . . .

A “modified” Fibonacci series uses starting numbers other than 0 and 1. For example, the starting number is 1 and 3, we will have a modified Fibonacci series as following:

1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843, 1364, 2207, 3571, 5778, 9349...

The modified Fibonacci series has been used in Phase I dose escalation study to determine the dose space.

Assuming the d1 is the starting dose for the first cohort, according to the modified Fabonacci series, the next dose cohort will be d2=2d1, and then d3=1.67d2, d4=1.5d3,... If the start dose is 5 mg and a study with 5 cohorts, the dose schema will be:

Cohort 1 (5 mg) -> Cohort 2 (10 mg) -> Cohort 3 (15 mg) -> Cohort 4 (25 mg) -> Cohort 5 (40 mg)

As we can see, with the dose increase, the ratio between two consecutive doses are getting smaller and smaller.

Further reading on the modified Fabonacci series and its application in dose escalation studies:

• Christophe Le Tourneau, J. Jack Lee, Lillian L. Siu (2009 JNCI) Dose Escalation Methods in Phase I Cancer Clinical Trials
• Phase I Clinical Trial Design by Lawrence V Rubinstein and Richard M Simon
• George Omura (2003) Modified Fibonacci Search Journal of Clinical Oncology

Odds Ratio and Relative Risk

Odds Ratio (OR) and Relative Risk (RR) are two ratios often used in the epidemiology studies and the clinical trials. They are related, but the calculation and the interpretation are quite different. Notice that the Relative Risk (RR) may also be called Risk Ratio with the same abbreviation of RR.

Relative Risk

P0=The probability of events (eg., responder, cardiovascular event) when a covaraite is at a give level (eg, treatment = Placebo, gender=female)
P1=The probability of events (eg., responder, cardiovascular event) when a covariate is at one unit higher than the previous level (eg., treatment = New Drug) or simply another level (gender=male)
RR = P1 / P0

Odds Ratio
Odds = The probability of events / the probablity of non-events
OR = Odds in one group / odds in another group = P1/((1-P1) divided by P0/(1-P0)
For example, OR = Odds in treated group / Odds in Placebo group

When P1 and P0 are small, OR can be used to estimate RR. However, then P1 and P0 are close to 0.5, the OR is typically much larger than RR.

Steve Simon wrote an excellent web page about the comparison of Odds Ratio versus Relative Risk.

In epidemiology class, we are typically advised to use OR for case-control study and use RR for cohort study. For cross-section studies, both OR and RR may be used.

In clinical trial setting, there is no consensus of using OR or RR. In practice, both of them are used. Sometimes, using OR or RR could be manipulated to serve one purpose or another. Brian Attig and Alison Clabaugh criticized the misuse of statistical interpretation of the odds ratio in APPLIED CLINICAL TRIALS.

Both OR and RR can be easily obtained from SAS Proc Freq with RISKDIFF option. An example by Mimi Chong from the following website illustrates this. We just need to be careful when we read the results from the SAS outputs. Odds ratio is clearly labelled and the Risk ratio is the the numbers corresponding to 'Col1 Risk' or 'col 2 risk' depending on which column is defined as 'event'.

If additional covariates (or in epimiology term, confounding factors) need to be considered, SAS Proc Freq with CMH option or Proc Logistic regression or Proc Genmod can be used.

The interactive voice response system

Interactive Voice Response (IVR) is an interactive technology that allows a computer to detect voice and keypad inputs. Its use in clinical trial probably started with the randomization. It replaces the old way in handling the randomization (i.e., through concealed envelopes). It makes the central randomization feasible and make it easy for handling the complex randomization schedules such as the randomization with multiple layers of stratefications and the randomization with dynamic allocation.


Currently most sponsors perform randomization using an Interactive Voice Response System (IVRS) so that treatment codes for individual patients are no longer available at the sites for inspection.


The IVRS utilizes a dynamic randomization system using an adaptive minimization technique for pre-specified stratification variables. The randomization algorithm evaluates previous treatment assignments across the different strata to determine the probability of treatment assignment. There are no fixed randomization lists available prior to enrollment of patients and there are no pre-determined randomization schedules. The randomization algorithm is the source document and is supposed to be signed and dated prior to the time when the first patient is randomized into the study. An external vendor is used to manage the treatment allocation codes. Once a subject is found to be eligible for a trial, the investigator contacts the IVRS vendor and provides details about the subject including their stratification factors. Typically sites receive confirmation faxes from the IVRS vendor that include relevant patient information such as the date of randomization, the date of last visit and the date the last medication was assigned.


In emergences, investigators must call the IVRS vendor to break the treatment code since there are no longer envelopes with patient numbers and treatment codes for investigators to open at the sites. Treatment codes may be released to external vendors prior to the final analysis in order for plasma concentration analyses or PK modeling to be performed in patients receiving the new investigational treatment. Treatment codes may also be released or partially broken up to the code level (e.g. treatment A, B) for the Data Safety Monitoring Board (DSMB) and may be completely unblinded if the chairman of the DSMB requests it. Treatment codes are released to the sponsor or contract research organization after the official analysis database lock.



Nowadays, the IVRS moves to the web-based system. The term is also becoming IWRS (interactive web response system). It could be the situation, when we use the term IVRS, it actually means IWRS.



The utility of the IVRS/IWRS is not just limited to the randomization. It can be used in other areas as well:

• Collecting the clinical efficacy outcome. For example, in IBS (Irritable Bowel Syndrome) study, the IVRS is used to collect the information about the presence or intensity of several IBS related symptoms daily (such as satisfactory relief, Abdominal discomfort or pain, Bloating, Stool frequency, Stool consistency...)
• Patient Reported Outcome (ePRO)
• Outcome research
• Cohort management (open/close a cohort) in dose-escalation studies
• Patient registry / registry studies
• Drug supply managment / Study drug inventory tracking

Spaghetti Plot

The first time when I used the term "Spaghetti" was for one of the pharmacokinetic studies where I would like to see the time-concentration curves for all individuals plotted on the same panel. The figure on the right side is an example of a Spaghetti plot from simulated data.

I don't think there is any formal definition for Spaghetti Plot, but this term refers to the plot for visualizing the trajectories for all individual subjects. The name “spaghetti plot” is called because it looks a bit like spaghetti noodles thrown on a wall.



The funny thing is that one time when I used the term 'spaghetti plot', I was asked not to use this term since it sounded like 'not formal'. Instead of using 'spaghetti plot', I had to change it to 'indivudual plots' or something like that. As a matter of fact, this term is actually used pretty often in pharmacokinetic studies and also in longitudinal studies.

In longitudinal studies, the spaghetti plot is used to visualize the trajectories or patterns or time trends. The spaghetti plot is typically used in the situation that the # of subjects is not too large and is generated for each group (if there is two treatment groups, there will be one spaghetti plot for each treatment group).

Spaghetti plot can be easily generated by software such as R and SAS. In SAS, the following statement can be used:

symbol1 value = circle color = black interpol = join repeat = 5;
proc gplot;
plot y*time = id / nolegend;
run;

Where y is the desired variable we would like to visualize; time is the time or visit; id is the subject #.

Some further readings:
1. UCLA: How can I visualize longitudinal data in SAS?
2. A oral contraceptive drug interaction study
3. A lecture notes by derived variable summaries
4. Quantitative Methods for Tracking Cognitive Change 3 Years After CABG

Williams Design

Williams Design is a special case of orthogonal latin squares design. It is a high-crossover design and typically used in Phase I studies. Due to the limitation of the # of subjects, we would like to achieve the balance and maximize the comparisons with the smallest # of subjects.

A Williams design possesses balance property and requires fewer sequences and periods. If the number of treatments (n) is an odd number, there will be 2 x n number of sequences. If the number of treatments (n) is an even number, there will be n number of sequences. The example below is a Williams Design with a 4 by 4 crossover (four treatments, four sequences, and also four periods).

Let A, B, C, and D stand for four different treatments, a Williams Design will be arranged as:

A D B C
B A C D
C B D A
D C A B

Notice that each treatment only occurs one time in one sequence, in one period. Furthermore, each treatment only follow another treatment one time. For example, treatment D following treatment B only one time in all sequences.

Several years ago, I wrote a paper on generating the randomization schedule using SAS. I illustrated an example for Williams Design.

There is a new paper by Wang et al specifically discussing about "The Construction of a Williams Design and Randomization in Cross-Over Clinical Trials using SAS"

Williams Design is deliberated in detail in the books "Design and Analysis of Clinical Trials" and Design and Analysis of Bioavailability and Bioequivalence Studies" by Chow and Liu

Williams Design is not purely used in Phase I or bioavailabity studies. I participated in a study with drug abuse area where a Williams design was used. It looks like that other people also uses Williams Design in drug abuse research.

Protocol Amendment after IND

In clinical development, filing of IND (Investigational New Drug) is an important milestone. FDA is required by the Modernization Act to respond in writing to an IND sponsor within 30 calendar days of receipt of the sponsor’s IND filing including the clinical study protocol(s). If the clinical study is not put on hold, the sponsor can start all clinical work including the patient enrollment.

After the initial IND is approved, how to oversee the IND if the sponsor makes significant changes to the study protocol?

First of all, any changes in the research protocol (protocol amendment or administrative letter) or patient informed consent form must be approved by the IRB (institutional Review Board) before the investigator or any sub-investigators put those changes into effect

Secondly, the protocol amendment needs to be submitted to FDA (immediately or through IND annual report). According to 21CFR312.30, the following requirements are stated:

"(b) Changes in a protocol. (1) A sponsor shall submit a protocol

amendment describing any change in a Phase 1 protocol that significantly
affects the safety of subjects or any change in a Phase 2 or 3 protocol
that significantly affects the safety of subjects, the scope of the
investigation, or the scientific quality of the study. Examples of
changes requiring an amendment under this paragraph include:
 (i) Any increase in drug dosage or duration of exposure of
individual subjects to the drug beyond that in the current protocol, or
any significant increase in the number of subjects under study.
 (ii) Any significant change in the design of a protocol (such as the
addition or dropping of a control group).
 (iii) The addition of a new test or procedure that is intended to
improve monitoring for, or reduce the risk of, a side effect or adverse
event; or the dropping of a test intended to monitor safety.
 (2)(i) A protocol change under paragraph (b)(1) of this section may
be made provided two conditions are met:
 (a) The sponsor has submitted the change to FDA for its review; and
 (b) The change has been approved by the IRB with responsibility for
review and approval of the study. The sponsor may comply with these two
conditions in either order.
 (ii) Notwithstanding paragraph (b)(2)(i) of this section, a protocol
change intended to eliminate an apparent immediate hazard to subjects
may be implemented immediately provided FDA is subsequently notified by
protocol amendment and the reviewing IRB is notified in accordance with
Sec. 56.104(c)."

IN FDA's compliance program guidance manual on 'clinical investigators and sponsor investigators', 

there are the following statements:

"Protocol changes/amendments. During the course of a study, a protocol may be formally changed 

by the sponsor. Such a change is usually prospectively planned and implemented in a systematic 

fashion through a protocol amendment. Protocol amendments must be reviewed and approved by 

the IRB, prior to implementation, and submitted to FDA. "

Not all protocol changes require the submission of a formal protocol amendment,
however, the sponsor's reporting responsibility depends on the nature of the
change.  In practice, many companies adopt a conservative approach by reporting
virtually all protocol changes.

Double Dummy Technique

Double dummy is a technique for retaining the blind when administering supplies in a clinical trial, when the two treatments cannot be made identical. Supplies are prepared for Treatment A (active and indistinguishable placebo) and for Treatment B (active and indistinguishable placebo). Subjects then take two sets of treatment; either A (active) and B (placebo), or A (placebo) and B (active).

Double dummy is a method of blinding where both treatment groups may receive placebo. For example, one group may receive Treatment A and the placebo of Treatment B; the other group would receive Treatment B and the placebo of Treatment A.

The figure on the left side is a double-dummy example for a two treatmetn arm scenario. The figure on the right side is a double-dummy example for a three-arm scenario. To maintain the blinding, subjects in each arm will take one tablet and one capsule. In the example on the right side table, subject in placebo arm will take one placebo tablet and one placebo capsule.

Group t-test or Chi-square test based on the summary data

Sometimes, the only data we have is the summary data (mean, standard deviation, # of subjects). Can we use the summary data (instead of the raw data) to calculate the statistical and p-values?

Yes, we can.

Below is an example for group t-test. I illustrate two methods for calculating the p-values based on the summary data.

In the method 1, we will use the SAS procedure PROC TTEST. The only trick thing is to enter the summary data in a data set with an SAS internal variable _STAT_ for the indicator of the summary statistics. The program below is self-explanatory.

data summary;
length _stat_ $4;
input week $ _STAT_ $ value@@;
datalines;
w1 n 7
w1 mean -2.6
w1 std 1.13
w2 n 5
w2 mean -1.2
w2 std 0.45
;
proc print;run;
proc ttest data=summary;
class week;
var value;
run;


Another way is to use the formula.


The correct formula for calculating the t value for group t-test is shown on the right side Where m=0 with degree freedom of n1+n2-2. To compare means from two independent samples with n1 and n2 observations to a value m, this formula can also be used.

where s**2 is the pooled variance

s**2 = [((n1-1)s1**2+(n2-1)s2**2)/(n1+n2-2)]

and s1**2 and s2**2 are the sample variances of the two groups. The use of this t statistic depends on the assumption that sigma1**2=sigma2**2, where sigma1**2 and sigma2**2 are the population variances of the two groups.

*Method #2;
data ttest;
input n1 mean1 sd1 n2 mean2 sd2;
s2 = (((n1-1)*sd1**2+(n2-1)*sd2**2)/(n1+n2-2));
s =sqrt(s2);
denominator = s * sqrt((1/n1) + (1/n2));
df = n1+n2-2;
t = (mean1 - mean2)/denominator;
p = (1-probt(abs(t),df))*2;
datalines;
7 -2.6 1.13
5 -1.2 0.45
;
run;
proc print;
run;

It will be even easier if the summary data is # of counts or frequency data. we can use SAS PROC FREQ option WEIGHT to indicate that data is for # of counts instead of the original individual data. The SAS codes will be something like:

data disease;
do exposure=1 to 2;
do disease=1 to 2;
input index@;
output;
end;
end;
cards;
23 32
17 15
;
proc freq data=disease;
tables exposure*disease/chisq;
weight index;
run;

Pharmacokinetics: Verify the Steady State Under Multiple Doses

For a multiple-dose regimen, the amount of drug in the body is said to have reached a steady state level if the amount or average concentration of the drug in the body remains stable. At steady state, the rate of elimination = the rate of administration.

To determine whether the steady state is achieved, statistical test can be performed on the trough levels. The predose blood sampling should include at least three successive trough level samples (Cmin).

In FDA's guidance for industry: Bioequivalence Guidance, it stated "...to determine a steady state concentration, the Cmin values should be regressed over time and the resultant slope should be tested for its difference from zero." For example, we can use the logarithm of last three trough measurements to regress over time. If the 90% CI for the exponential of slope for time is within (0.9, 1.1), then we will claim SS. The limit of (0.9, 1.1) is arbitrarily decided.


Similarly, in FDA's guidance for Industry: Clozapine Tablets: In Vivo Bioequivalence and In Vitro Dissolution Testing, it stated "...The trough concentration data should also be analyzed statistically to verify that steady-state was achieved prior to Period 1 and Period 2 pharmacokinetic sampling."

Typically, the verification of the steady state can simply be the review of the trough levels at time points prior to the PK sampling without formal statistical testing. If the PK blood samples are taken after 4-5 dose intervals, it can be roughly assumed that the (approximately or near) steady state has been reached.
The trough and peak values of plasma concentrations are also used to determine whether the steady state has been reached. The peak to trough ratio is usually used as an indicator of fluctuation of drug efficacy and safety. A relatively small peak to trough ratio indicates that the study drug is relatively effective and safe.

In their book "Design and analysis of bioavailability and bioequivalence studies", Chow and Liu described the univariate analysis and multivariate anaysis approaches to test the steady state formally.

Hong also proposed a non-linear procedure to test for steady state.

A note about trough and Cmin:

The characteristic Cmin has been associated with the concentration at the end of te dosing interval, the so-called pre-dose or trough value. However, for prolonged release formulations which exhibit an apparent lag-time of absorption, the true minimum (trough) concentration may be observed some time after the next dosing, but not necessarily at the end of the previous dosing interval.

Statistical validation of the surrogate endpoints

A surrogate endpoint is intended to substitute for a clinical endpoint. A surrogate endpoint is expected to predict clinical benefit (or harm, or lack of benefit) based on epidemiologic, therapeutic, pathophysiologic or other scientific evidence. In clinical trials, a surrogate endpoint (or marker) is a measure of effect of a certain treatment that may correlate with a real endpoint but doesn't necessarily have a guaranteed relationship. The National Institutes of Health (USA) define surrogate endpoint as "a biomarker intended to substitute for a clinical endpoint"

Biomarkers are biological substances or features that can be used to indicate normal biological processes, disease processes, or responses to therapy. Biomarkers can be physiological indicators, such as heart rate or blood pressure, or they can be molecules in the tissues, blood, or other body fluids. For example, elevated blood levels of a protein called prostate specific antigen is a molecular biomarker for prostate cancer.

Biomarker and surrogate endpoint are often used interchangeably. However, there a subtle difference. Surrogate endpoints may not just be biomarkers and could include the imaging measurements (such as CT bone/lung densitometry, arteriogram...).

Just recently, I noticed that there are quite some works done in the area of statistical validadtion for surrogate endpoints. In the medical community, people may simply think that a biomarker can be a surrogate endpoint if the correlation between a surrogate endpoint and an established clinical endpoint are observed. However, the correlation is only one of the criteria (or requirement) for a biomarker to be a valid surrogate endpoint. To validate a surrogate endpoint, there have been a lot of discussions about the statistical approach in validating the surrogate endpoint.

in their paper titled "Surrogate end points in clinical trials: are we being misled?" (1996), Fleming and DeMets provided many examples of the surrogate endpoints and pointed out that these surrogate endpoints often fail in formal statistical validation.

The issues with surrogate endpoint is actually discussed in ICH E9 Statistical Principles for Clinical Trials

Surrogate Variables (2.2.6)
When direct assessment of the clinical benefit to the subject through observing
actual clinical efficacy is not practical, indirect criteria (surrogate variables — see
Glossary) may be considered. Commonly accepted surrogate variables are used in
a number of indications where they are believed to be reliable predictors of
clinical benefit. There are two principal concerns with the introduction of any
proposed surrogate variable. First, it may not be a true predictor of the clinical
outcome of interest. For example, it may measure treatment activity associated
with one specific pharmacological mechanism, but may not provide full information
on the range of actions and ultimate effects of the treatment, whether positive or
negative. There have been many instances where treatments showing a highly
positive effect on a proposed surrogate have ultimately been shown to be
detrimental to the subjects' clinical outcome; conversely, there are cases of
treatments conferring clinical benefit without measurable impact on proposed
surrogates. Second, proposed surrogate variables may not yield a quantitative
measure of clinical benefit that can be weighed directly against adverse effects.
Statistical criteria for validating surrogate variables have been proposed but the
experience with their use is relatively limited. In practice, the strength of the
evidence for surrogacy depends upon (i) the biological plausibility of the
relationship, (ii) the demonstration in epidemiological studies of the prognostic
value of the surrogate for the clinical outcome, and (iii) evidence from clinical
trials that treatment effects on the surrogate correspond to effects on the clinical
outcome. Relationships between clinical and surrogate variables for one product
do not necessarily apply to a product with a different mode of action for treating the
same disease.

Some key references:
1. Prentice, R. L. (1989). Surrogate endpoints in clinical trials: Definition and operational criteria. Statistics in Medicine 8 431–440
2. Freedman L, Graubard B (1992). Statistical validation of intermediate endpoints for chronic
diseases. Statistics in Medicine
3. Lin DY, Fleming TR, DeGruttola V. (1997) Estimating the proportion of treatment effect explained by a surrogate endpoint. Statistics in Medicine, 16:1515-1527
4. A framework for biomarker and surrogate endpoint in drug development by Janet Woodcock
5. Surrogate Markers - Their Role in Regulatory Decision Process
6. Statistical Validadtion of surrogate markers
7. Fleming and DeMets (1996) Surrogate End Points in Clinical Trials: Are We Being Misled? Ann Mem Med. 1996; 125:605-613

Imaging analysis in clinical trial

Medical imaging has now been a critical part in clinical trials. It can be used in many aspects of clinical trial process:
1) Disease diagnosis as part of inclusion/exclusion criteria
2) Safety assessment
3) Clinical efficacy endpoint

There are many medical imaging technologies. Here are just a list of some:
1) x-ray
2) CT scan
3) MRI
4) PET scan
5) Ultrasound
6) arteriogram or angiography
7) venogram

There is benefit and risk in using the medical imaging in clinical trials. Some imaging can pose extra safety issues. For example, x-ray, CT scan, PET scan can put the study subjects at extra radiological exposure. Arteriogram and CT/A can expose the subjects to additional contrast medium or dyes which may have its own safety issue.

Medical imaging is always a surrogate endpoint. The technician plays the important role in obtaining the imaging. The standardization and calibration are always important in order to obtain the reliable data especially in longitudinal studies. The interpretation of the imaging results depend on who read the imaging. There could be substantial variation between different readers. Therefore, the central reading is very important if the medical imaging is used in clinical trial. There are quite some articles discussing the imaging in clinical trials in the Applied Clinical Trial magazine.

There are several specialty medical imaging vendors on the market. Some of them are listed below:
1) BioClinica or Bio-imaging
2) Biomedical Systems
3) Perceptive (part of Parexel)
4) Synarc

FDA and EMEA has issued several guidance on imaging used in clinical trial. For example:

1) FDA Guidance "Standards for Clinical Trials Imaging Endpoints"
This guidance discussed the clinical trials with imaging endpoints - i.e., the reading from medical imaging is used as the efficacy endpoint. Examples are: RECIST criteria for assessing the tumor size for solid tumor based on FDG-PET or MRI. Lung density measure by CT scan to assess emphysema.

2) FDA guidance Developing Imaging Drug and Biological Products,

• Part 1: Conducting Clinical Safety Assessments) (Imaging Drug Guidance Part 1) ;
• Part 2: Clinical Indications (Imaging Drug Guidance Part 2);
• Part 3: Design, Analysis and Interpretation of Clinical Studies (Imaging Drug Guidance Part 3)

3) FDA guidance on "New Contrast Imaging Indication Considerations for Devices and Approved Drug and Biological Products"

4) Developing Medical Imaging Drugs and Biologics

5) EMEA Concept Paper on "The Harmonisation and Update of the Clinical Aspects in the Authorised Conditions of Use for Radiopharmaceuticals and Other Diagnostic Medical Products"

Additional reading:

• Medical imaging in clinical trials
• Cancer Imaging Clinical Trials
• Cancer Imaging Program
• Diagnostic Imaging

Adjustment for multiplicity

one of the issues in statistics field is the adjustment for multiplicity - adjustment of alpha level for multiple tests. The multiplicity can arise in many different situations in clinical trials; some of them are listed below:

• Multiple arms
• Co-primary endpoints
• Multiple statistical approaches for the same endpoint
• Interim analysis
• More than one doses vs. Placebo
• Meta analysis
• Sub group analysis

There are tons of articles about the multiplicity, but there are few guidances from the regulatory bodies. While the multiplicity issues arise, the common understanding is that the adjustment needs to be made. However, there is no guidance on which approach should be used. The adjustment approach could be the very conservative approach (e.g., Bonferroni) or less conservative (e.g., Hochberg). One could evaluate the various approaches and determine which adjusmtent approach is best suited to the situation in study.

While we are still waiting for FDA's guidance on multiplicity issue (hopefully it will come out in 2009), EMEA has issued a PtC (point to consider) document on multiplicity. The document provide guidances on when an adjustment for multiplicity should be implemented.

While there are so many articles related to multiplicity, I find the following articles suitable for my taste and with practical discussions.

• Proschan and Waclawiw (2000) Practical Guidelines for Multiplicity Adjustment in Clinical Trials. Controlled Clinical Trial
• Capizzi and Zhang (1996) Testing the Hypothesis that Matters for Multiple Primary Endpoints. Drug Information Journal
• Koch and Gansky (1996) Statistical Considerations for Multiplicity in Confirmatory Protocols. Drug information Journal
• Wright (1992) Adjust p values for simutaneous inference. Biometrics

It is always useful to refer to the statistical review documents for previous NDA/BLA to see which kind of approaches have been used in drug approval process. Three approaches below seem to stand out. These three approaches are also mentioned in

• Hochberg procedure
• Bonferroni-Holm procedure
• Hierarchical order for testing null hypotheses

while not exactly the same, In a CDRH guidance on

"Clinical Investigations of Devices Indicated for the Treatment of Urinary Incontinence ", it states “The primary statistical challenge in supporting the indication for use or device performance in the labeling is in making multiple assessments of the secondary endpoint data without increasing the type 1 error rate above an acceptable level (typically 5%). There are many valid multiplicity adjustment strategies available for use to maintain the type 1 error rate at or below the specified level, three of which are listed below:
· Bonferroni procedure;
· Hierarchical closed test procedure; and
· Holm’s step-down procedure. "

Hochberg procedure is based on Hochberg's paper in 1988. It has been used in several NDA/BLA submissions. For example, in Tysabri BLA, it is stated

"Hochberg procedure for multiple comparisons was used for the evaluation of the primary endpoints. For 2 endpoints, the Hochberg procedure results in the following rule: if the maximum of the 2 p-values is less than 0.05, then both hypotheses are rejected and claim the statistical significance for both endpoints. Otherwise, if the minimum of the 2 p-values needs to be less than 0.025 for claiming the statistical significance".

Bonferroni-Holm procedure is based on Holm's paper in 1979 (Holm, S (1979): "A simple sequentially rejective multiple test procedure", Scandinavian Journal of Statistics, 6:65–70). It is a modification to the original method. This method may also be called Holm-Bonferroni approach or Bonferroni-Holm correction. This approach was employed in Flomax NDA (020579). and BLA for HFM-582 (STN 125057).

Both Holm's procedure and Hochberg's procedure are the modifications from the Bonferroni procedure. Holm's procedure is called 'step-down procedure' and Hochberg's procedure is called 'step-up procedure'. An article by Huang and Hsu titled "Hochberg's step-up method: cutting corners off Holm's step-down method" (Biometrika 2007 94(4):965-975) provided a good comparison of these two procedures.

Benjamin-Hochberg also proposed a new procedure which controls the FDR (false discovery rate) instead of controling the overall alpha level. The original paper by Benjamin and Hochberg is titled "controlling the false discovery rate: a practical and powerful approach to multiple testing" appeared in Journal of the Royal Statistical Society. it is interesting that the FDR and Benjamin-Hochberg procedure has been pretty often used in the gene identification/microarray area. A nice comparison of Bonferroni-Holm approach and Benjamin-Hochberg approach is from this website. Another good summary is the slides from 2004 FDA/Industry statistics worshop.

Hierarchical order for testing null hypotheses was cited in EMEA's guidance as

"Two or more primary variables ranked according to clinical relevance. No formal adjustment is necessary. Howeveer, no confirmatory claims can be based on variables that have a rank lower than or equal to that variable whose null hypothesis was the first that could not be rejected. "

This approach can be explained as a situation where a primary endpoint and several other secondary endpoints are defined. The highest ranked hypothesis is similar to the primary endpoint and the lower ranked endpoints are similar to the secondary endpoints.

In one of my old studies, we hypothsized the comparisons as something like below:

"A closed test procedure with the following sort order will be used for the pairwise comparisons. The second hypothesis will be tested only if the first hypothesis has been rejected, thus maintaining the overall significance level at 5%.
1. The contrast between drug 400mg and placebo (two-sided, alpha = 0.05)(H01 : mu of 400 mg = mu of placebo)
2. The contrast between drug 400 mg and a comparator (two-sided, alpha = 0.05)(H02 : mu of 400 mg = mu of the comparator) "

Understanding person-year or patient-year

When I studied the public health many years ago, in occupational health class, the term 'person year' was pretty often used. Since the length of exposure to the health hazard is different for different workers, it is necessary to calculate the person year. The total person year (summation of person year from all workers exposed to certain industry hazard) will then be used to calculate the rate (such as death rate, mortality rate,...). When same logic is used in the clinical setting or in clinical trial field, the similar term 'patient year' is used. The terms 'person year' and 'patient year' are used interchangeably.

The rates are represented as “per person-time” to provide more accurate comparisons among groups when follow-up time (i.e., patient exposure time) is not the same in all groups. Theoretically, we can express a rate of events per patient year, but the rate would be typically be a fraction or too small. In practice, the rate can be expressed as per 100, 1000, 100,000, 1 million patient-years or patient-years at risk.

“Patient-year at risk” means that the denominator of the rate calculation is ascertained by adding exposure times of all patients, where each patient’s exposure time is defined as days spent in a pre-determined time period (i.e., a year), censored only by events such as death or disenrollment, or the end of the time period. Divide the total number of days by 365 or 365.25 to get the actual year value.

“Patient-year” means that the denominator of the rate calculation is ascertained by counting all patients who are in the pre-determined time period for at least one day.

The expressions “per 100,000 patient-years at risk” and “per million patient-years” are just different ways of normalizing the rates to better present them. Thus, a hospitalization rate of 0.0000015 per patient-year, can also be expressed as 1.5 per million patient-years.

CTSpedia.org provided pretty detail explanation about the person-time (person year is just a special case of the person-time). An example of calculating death rate using patient year is illustrated from Organ Donor website.

The rate expressed in 'patient year' has been used in many different scenarios. For example, the following paragraph from a website have used 'The number of exacerbations per patient year'; 'the number of exacerbation days per patient year',...

"Additionally, tiotropium significantly reduced the number of exacerbations (0.853 vs 1.051 exacerbations per patient-year; p=0.003) (1) and number of exacerbation days (mean: 12.61 vs 15.96 days per patient year; p is less than 0.001). Similarly, tiotropium significantly reduced the frequency of exacerbation related hospitalizations (0.177 vs 0.253 means hospitalizations per patient year, p=0.013)(1) and the number of hospitalization days (1.433 vs. 1.702, mean days per patient year, p=0.001) compared to placebo. In addition, a reduction in the number of treatment days (antibiotic or steroids) (p is less than 0.001) and unscheduled visits to health care providers for exacerbations (p = 0.017) were also significantly reduced with tiotropium compared to placebo."

In FDA guidance "Efficacy, Safety, and Pharmacokinetic Studies to Support Marketing of Immune Globulin Intravenous (Human) as Replacement Therapy for Primary Humoral Immunodeficiency", the rate of SBI (serious bacterial infection) is per person-year.

"The protocol should prospectively define the study analyses. We expect that the data analyses presented in the BLA will be consistent with the analytical plan submitted to the IND. Based on our examination of historical data, we believe that a statistical demonstration of a serious infection rate per person-year less than 1.0 is adequate to provide substantial evidence of efficacy. You may test the null hypothesis that the serious infection rate is greater than or equal to 1.0 per person-year at the 0.01 level of significance or, equivalently, the upper one-sided 99% confidence limit would be less than 1.0. "
"We recommend that you provide in the BLA descriptive statistics for the number of serious infection episodes per person-year during the period of study observation."

Acronym related to Clinical trials in EU countries

In order to conduct a clinical trial in the EC, the sponsor must first submit a valid request for authorisation to the Competent Authority of the Member State where they propose to conduct the trial. This request is known as the Clinical Trial Application (CTA). The content of this application will then be assessed by the competent authority and/or the Ethics Committee to ensure that the anticipated therapeutic benefits to the patient justify any foreseeable risks before a favourable opinion is issued to allow the trial to proceed.

The safety of subjects participating in a clinical trial is the main reason behind many of the changes brought about by the Directive and thus why the need for a common system of authorization has also come about. This requirement within the pharmaceutical industry was previously only applicable to commercial products. However, this change now means that all facilities used for the manufacture or import of Investigational Medicinal Products (IMPs) will be subject to an inspection by the competent authority.

This is to ensure that the principles of Good Manufacturing Practice (GMP) as led down in Annex 13 to the EU guide to Good Manufacturing Practice are being adhered to. On the basis of this inspection, they may become licensed by the competent authority. This authorisation takes the form of a Manufacturing Authorisation for IMPs or MA for IMPs.

Yet, one additional aspect must be fulfilled in order for a facility to be granted a licence. This is the need for the manufacturer or importer to have a Qualified Person (QP) permanently and continuously at their disposal. This person will be named on the licence and will be responsible for the release of batches of clinical trial material before they can be used in a clinical trial.

Several scenarios present themselves. The first one is when the IMP has been manufactured within Europe. This is no doubt the simplest case for the QP when discharging their duties. In order to release material of European origin, they must confirm that each batch has been manufactured and checked in compliance with GMP, the Product Specification File (PSF) and the request for authorisation to conduct the trial, i.e. the CTA.

Another scenario exists when a comparator product from outside the EU, with a marketing authorisation (MA) in that country is to be used as an IMP. Under such circumstances the QP can perform release, if documentation is available to certify its manufacture to standards at least equivalent to European GMP. However, in the absence of such documentation, the QP must ensure that each lot undergoes all relevant analyses, tests or checks to confirm its quality.

This can sometimes prove difficult and therefore it is important that the sponsor gives purchase of comparators due consideration. One piece of advice would be that, if possible, comparators should be sourced within Europe or from countries where Mutual Recognition Agreements are already in existence, such as Canada, Australia, New Zealand, Switzerland and Japan. These Mutual Recognition Agreements are based on trust and confidence and are therefore very useful when it comes to importing comparators, as they aim to remove barriers to trade and promote standardization of GMP.

MA: Marketing authorization

MAH: Marketing authorization holder

CA: Competent Authority

QP: Qualified Person

MRP: Mutual Recognition Process

MRA: Mutual Recognition Agreement

EMEA: European Medicines Agency

• The European Medicines Agency (EMEA) is a decentralised body of the European Union with headquarters in London. Its main responsibility is the protection and promotion of public and animal health, through the evaluation and supervision of medicines for human and veterinary use.

BPWP: blood product working party

• The Blood Products Working Party (BPWP) was set up by the CHMP to provide recommendations on all matters relating directly or indirectly to efficacy and safety aspects of blood products.

CHMP: The Committee for Medicinal Products

• The Committee for Medicinal Products for Human Use (CHMP) is responsible for preparing the Agency's opinions on all questions concerning medicinal products for human use, in accordance with Regulation (EC) No 726/2004.

NfG: Notes for Guidance

PtC: Point to Consider

PEI: paul-Enrlich-Institut

The Paul-Ehrlich-Institut is an institution of the Federal Republic of Germany. It reports to the Bundesministerium für GesundheitSimilar to CBER of FDA.
(Federal Ministry of Health).

RMS: Reference Member State

Concerned Member States

Application for variation to a marketing authorisation = sNDA or sBLA

MHRA: Medicines and Healthcare products Regulatory Agency - An executive agency of the Department of Health in UK - simiar to FDA in US

SPC or SmPC: Summary of Product Characteristics - similar to Label or Package Insert in US.

• Pescription medications are regulated by governmental bodies to assure quality and appropriate use. In the US, the FDA regulates medications, and requires "labels" to be approved. "Package inserts" are written for health care providers. They contain very detailed information about different drugs. Frequently, there are also official documents for patients, called Patient Information leaflets. The manufacturers prepare this information, and the FDA approves it (sometimes after considerable discussions and negotiations!).
• In Europe, a similar process is used, with the "label" called the Summary of Product Characteristics (SPC, or SmPC). The patient-oriented document is called a "Package Leaflet" or "Patient Information Leaflet" (PILs)
  

IPMD: The Investigational Medicinal Product Dossier (IMPD)- similar to IND submission in US. IMPD needs to be submitted to the concerned competent authority (CA) in order to obtain the authorization of conducting the clinical trial.

CTA: Clinical Trial Application - similar to IND (investigational new drug)

NICE: The National Institute for Health and Clinical Excellence a counterpart in US is the Agency for Healthcare Research and Quality.

• NICE is a special health aurhority of the National Health Service (NHS) in England and Wales. It was set up as the National Institute for Clinical Excellence in 1999, and on 1 April 2005 joined with the Health Development Agency to become the new National Institute for Health and Clinical Excellence (still abbreviated as NICE).
• NICE publishes clinical appraisals of whether particular treatments should be considered worthwhile by the NHS. These appraisals are based primarily on cost-effectiveness.

For further reading:

• Navigating difference Between FDA and EMEA for Regulatory Compliance During Drug Development
• EMEA FDA CMC difference
• Navigating the global regulatory pathway
  

Risk management, pharmacoepidemiology, and pharmacovigilence

Risk Management:
Risk management is the overall and continuing process of minimizing risks throughout a product's lifecycle to optimize its benefit/risk balance. Risk information emerges continuously throughout a product's lifecycle, during both the investigation and marketing phases through both labeled and off-label uses. FDA considers risk management to be a continuous process of (1) learning about and interpreting a product's benefits and risks, (2) designing and implementing interventions to minimize a product's risks, (3) evaluating interventions in light of new knowledge that is acquired over time, and (4) revising interventions when appropriate.

Pharmacoepidemiology:

pharmacoepidemiology is the study of the utilization and effects of drugs in large numbers of patients. It can be viewed as an epidemiological discipline with particular focus on drugs.The process of identifying and responding to safety issues about drugs.

Pharmacovigilance (PVG):
Pharmacovigilance is generally regarded as all postapproval scientific and data gathering activities relating to the detection, assessment, understanding, and prevention of adverse events or any other product-related problems. This includes the use of pharmacoepidemiologic studies.

Patient registry:
The term "registry" as used in pharmacovigilance and pharmacoepidemiology is often given different meanings. For the purpose of this concept paper, we are defining a registry as a systematic collection of defined events or product exposures in a defined patient population for a defined period of time. Through the creation of registries, a sponsor can monitor for safety signals identified from spontaneous case reports, literature reports, or other sources, and evaluate factors that affect the risk of adverse outcomes, such as dose, timing of exposure, or other patient characteristics.

REMS: Risk Evaluation and Mitigation Strategy

A Risk Evaluation and Mitigation Strategy (REMS) is a strategy to manage a known or potential serious risk associated with a drug or biological product. A REMS will be required if FDA finds that a REMS is necessary to ensure that the benefits of the drug or biological product outweigh the risks of the product, and FDA notifies the sponsor. A REMS can include a Medication Guide, Patient Package Insert, a communication plan, elements to assure safe use, and an implementation system, and must include a timetable for assessment of the REMS. Some drug and biological products that previously were approved/licensed with risk minimization action plans (RiskMAPs) will now be deemed to have REMS.

For more information, see FDA's website about FDAAA.

also, the following website may be useful:

• FDA workshop on risk management

• Global Risk Management


• in VIVO blog

Effect Size

Effect size (ES) is a name given to a family of indices that measure the magnitude of a treatment effect. Unlike significance tests, these indices are independent of sample size. Effect size has been frequently linked to the power analysis (or sample size calculation) and Meta analysis.

The concept of effect size seems to come from Cohen's book "Statistical Power Analysis for the Behavioral Sciences". Effect size is not just for the continuous variable, it could also be for rates and proportions, and other type of data.

The following weblinks provide good summaries on effect size:

• Effect size (ES)
• Effect Size Substantive Interpretation Guidelines: Issues in the Interpretation of Effect Sizes
• Power Analysis, Statistical Significance, & Effect Size
• Effect size on Wikipedia

Recently, I came across a paper that described the use of effect size as Benchmarks for Interpreting Change - one of many ways to determine the sensitivity of the measurement and subsequently the minimal clinically important difference (MCID) or minimal important difference (MID).

In a paper by Kazis LE, Anderson JJ, Meenan RF (Effect sizes for interpreting changes in health status. Med Care 1989;27:S178-S189), they described the following:

"Effect size as used in this study is calcu-lated by taking the difference between the means before treatment and after treatment and dividing it by the standard deviation of the same measure before treatment. This method of calculating effect sizes can be expressed mathematically as ES = (mi - m2)/sl, where m, is the pretreatment mean, m2 the posttreatment mean, and s, the pretreatment standard deviation. In this instance the before-treatment scores are used as a proxy for control group scores. This approach treats the effect size as a standard measure of change in a "before and after study" context. We are interested in the magnitude or size of the change rather than statistical significance, so we use the standard deviation at baseline rather than the standard deviation of the differ-ence between the means.8 Effect sizes can be used to translate changes in health status into a standard unit of measurement that will provide a clearer interpretation of the results. This can be ac-complished by using effect sizes as bench-marks for measuring changes or as a means for taking comparisons between measures in the same study or across studies. "

Here the effect size is not to compare the two treatmetn groups, rather compare the differences pre and post. The formula for effect size can be explicitly rewritten to represent the mean change from pre treatment to the post treatment divided by the standard deviation of the baseline measures (effect size = (mui - mu0/SDmu0; mui = mean value of the post-baseline measure; mu0 = mean value at baseline).

If we calculate the effect size for both treatment group and placebo group, we should expect a very small effect size for Placebo group and a rather large effect size for treatment group - an indicator of a good measurement.

Least squares means (marginal means) vs. means

If you work with SAS, you probably heard and used the term 'least squares means' very often. Least squares means (LS Means) are actually a sort of SAS jargon. Least square means is actually referred to as marginal means (or sometimes EMM - estimated marginal means). In an analysis of covariance model, they are the group means after having controlled for a covariate (i.e. holding it constant at some typical value of the

covariate, such as its mean value).

I often find that it is neccessary to use a very simple example to illulatrate the difference between LS Means and Means to my non-statistician colleagues. I made up the data in Table 1 above. There are two treatment groups (treatment A and treatment B) that are measured at two centers (Center 1 and Center 2).

The mean value for Treatment A is simply the summation of all measures divided by the total number of observations (Mean for treatment A = 24/5 = 4.8); similarly the Mean for treatment B = 26/5 = 5.2. Mean for treatmeng A > Mean for treatment B.

Table 2 shows the calculation of least squares means. First step is to calculate the means for each cell of treatment and center combination. The mean 9/3=3 for treatment A and center 1 combination; 7.5 for treatment A and center 2 combination; 5.5 for treatment B and center 1 combination; and 5 for treatment B and center 2 combination.

After the mean for each cell is calculated, the least squares means are simply the average of these means. For treatment A, the LS mean is (3+7.5)/2 = 5.25; for treatment B, it is (5.5+5)/2=5.25. The LS Mean for both treatment groups are identical.

It is easy to show the simple calculation of means and LS means in the above table with two factors. In clinical trials, the statistical model often needs to be adjusted for multiple factors including both categorical (treatment, center, gender) and continuous covariates (baseline measures). The calculation of LS mean is not easy to demonstrate. However, the LS mean should be used when the inferential comparison needs to be made. Typically, the means and LS means should point to the same direction (while with different values) for treatment comparison. Occasionally, they could point to the different directions (treatment A better than treatment B according to mean values; treatment B better than treatment A according to LS Mean).

SAS procedure GLM has a nice discussion about the comparison of Least Square Means vs. Means. A small article "Means vs LS Means and Type I vs Type III Sum of Squares"by Dan may also help.

Jadad Scale to assess the quality of clinical trials

In a cost-effectiveness assessment report, a detail descriptions were provided for the approaches in choosing the clinical trial data for meta analysis. After many clinical trials are selected, a 'Jadad Scale' was used to assess the quality of clinical trials.

Jadad Scale sometimes known as Jadad scoring or the Oxford quality scoring system, is a procedure to independently assess the methodological quality of a clincal trial. It is the most widely used such assessment in the world.

The Jadad score was used as the 'gold standard' to assess the methodological quality of studies. This validated score lies in the range 0-5. Studies are scored according to the presence of three key methodological features of randomization, blinding and accountability of all patients, including withdrawals.

According to NIH website Appendix E: The Jadad Score
A Method for assessing the quality of controlled clinical trials
Basic Jadad Score is assessed based on the answer to the following 5 questions.
The maximum score is 5.

Question Yes No
1. Was the study described as random? 1 0
2. Was the randomization scheme described and appropriate? 1 0
3. Was the study described as double-blind? 1 0
4. Was the method of double blinding appropriate? (Were both the patient and the assessor appropriately blinded?) 1 0
5. Was there a description of dropouts and withdrawals? 1 0

Quality Assessment Based on Jadad Score

Range of Score Quality
0–2 Low
3–5 High

Wikipedia has a pretty good summary of the use of Jadad Scale.

Jadad Scale has been frequently used as a study selection criteria when the literature review or meta analysis are performed.

References:
1. Jadad AR, Moore RA, Carroll D, et al. Assessing the quality of reports of randomized clinical trials: Is blinding necessary? Control Clin Trials 1996;17:1-12.

Stratified randomization to achieve the balance of treatment assignment within each strata

Stratified randomization refers to the situation in which strata are constructed based on values of prognostic variables or baseline covariates and a randomization scheme is performed separately within each stratum. One misconception is to think that the stratified randomization is going to require the equal number of subjects for each strata.

For example, suppose that in a two-arm, parallel design study, we would like to stratify the randomization for age group (<18 versus >=18 years old). But we don't know how many subjects in each age group we could enroll. The purpose is to make sure that within each age group, there are equal numbers of subjects assigned to treatment A or treatment B.

After the study, there may be quite different total number of subjects in each age group, but within each age group, there should be approximately equal number of subjects in treatment A or treatment B.

The strata size usually vary (maybe there are relatively fewer young males and young females with the disease of interest). The objective of stratified randomization is to ensure balance of the treatment groups with respect to the various combinations of the prognostic variables. Simple randomization will not ensure that these groups are balanced within these strata so permuted blocks are used within each stratum are used to achieve balance.

When the stratified randomization is utilized, the # of stratification factors is typically limited to 1 or 2. The number of strata is exponentially increased if too many randomization factors are included. For example, if we have 4 stratification factors and each factor has two levels, then the # of strata = 2^4 = 16 strata, which is not practical.

If there are too many strata in relation to the target sample size, then some of the strata will be empty or sparse. This can be taken to the extreme such that each stratum consists of only one patient each, which in effect would yield a similar result as simple randomization. Keep the number of strata used to a minimum for good effect.

I have also seen a trial to require the equal number of subjects for each strata and with each strata, then equal number of subjects assigned to two treatment groups. In a trial to study the IBS (irritable bowel Syndrome), the protocol required the equal number of subjects in two type of IBSs (IBS-C vs. IBS-M). Within IBS-C or IBS-M group, there should be equal number of subjects assigned to treatment A or treatment B. The things turned out not nice because there were a lot of more subjects with IBS-C than IBS-M. During the study, while enrollment target for IBS-C was achieved, there was still a lot of IBS-M subjects to be enrolled.

IBS-C=Irritable Bowel Syndrome (constipation dominant)
IBS-M=Irritable Bowel Syndrome (mixed - constipation and diarrria)